
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Der Untergrund von Beugungsfiguren
Der Untergrund von Beugungsfiguren wurde in Abhängigkeit von Spaltweite, Entfernung, Divergenz der Beleuchtung und in Fresnelscher- und Fraunhoferscher Beobachtungsart untersucht. Der Untergrund ist höher bei großen Spaltweiten und nimmt nicht proportional der Entfernung ab, sondern langsamer. Die Differenz der Maxima und Minima ist annähernd unabhängig von der Spaltweite entsprechend der Beobachtung von Newton, daß gebeugtes Licht nur aus einer engen Umgebung der Kante kommt.
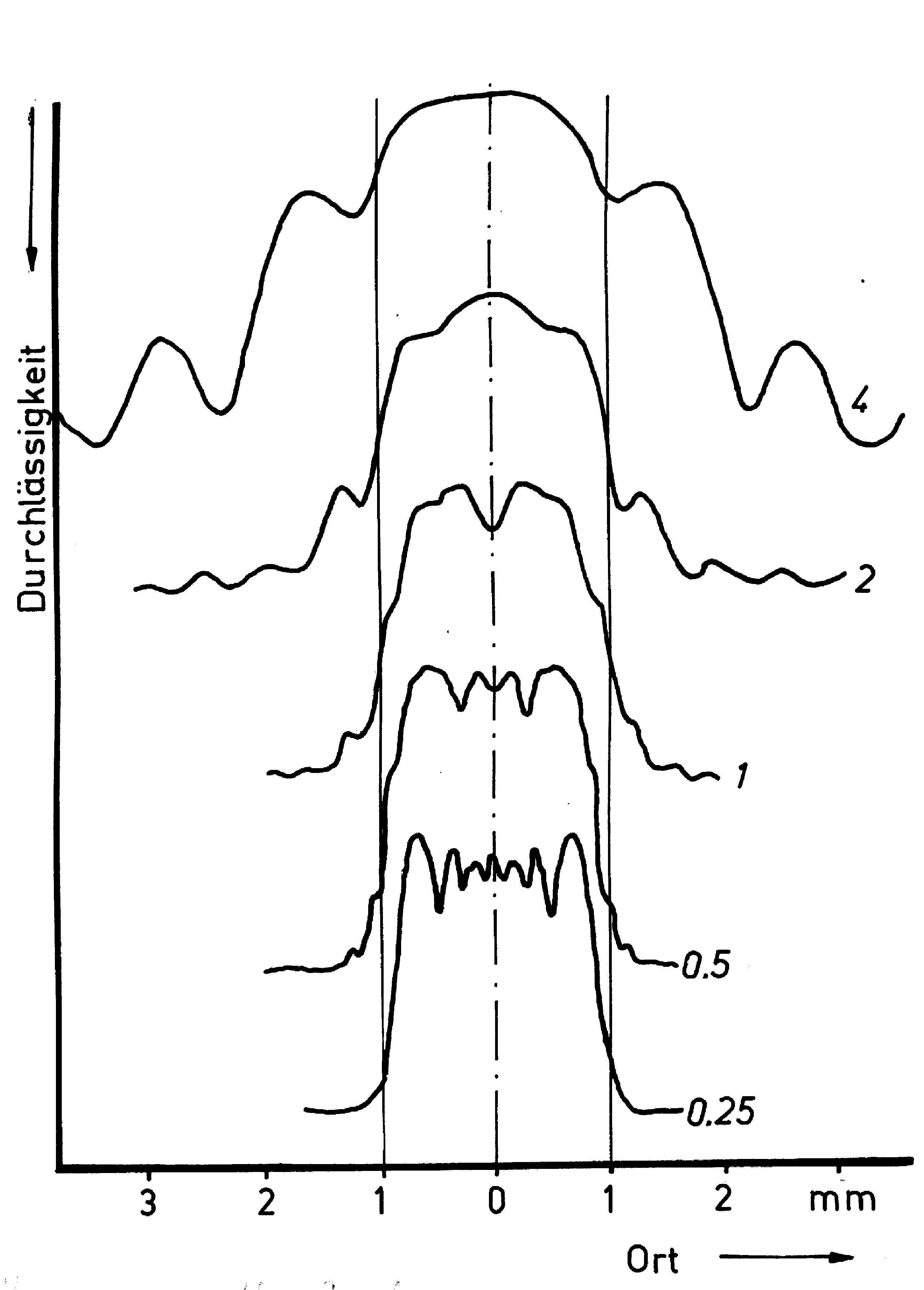
Abb. 1. Beugungsfigur eines Spaltes der Weite 2 mm in Abhängigkeit von der Entfernung bei Beleuchtung mit parallelem Licht. Es ist die Durchlässigkeit der Negative in Abhängigkeit vom Ort aufgetragen. Die Schattengrenze von 2 mm Breite ist durch zwei vertikale Linien gekennzeichnet. Die angeschriebenen Zahlen weisen auf die Entfernung Spalt - Photofilm in Meter.
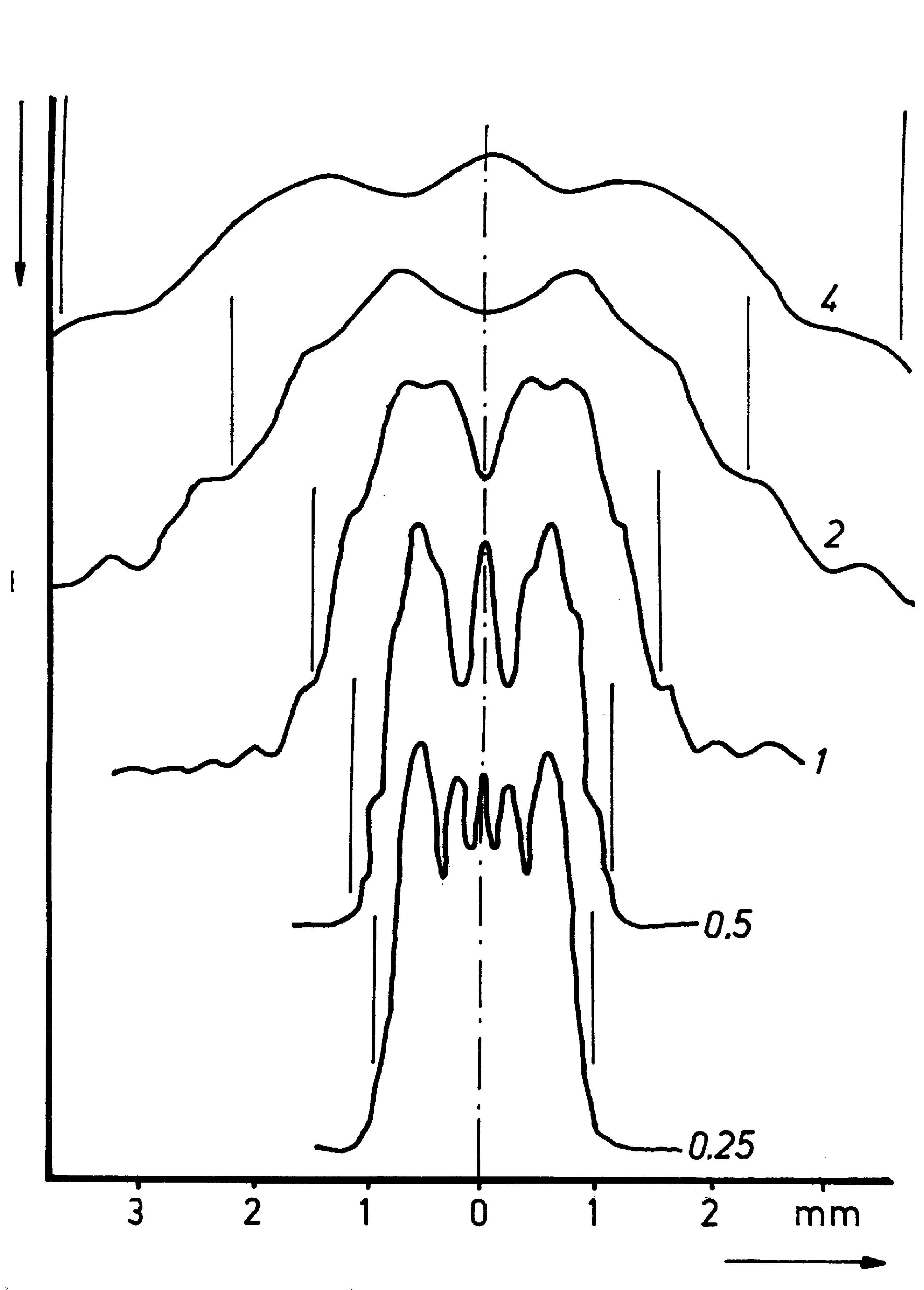
Abb. 2. Wie Abb. 1, aber die Sammellinse f' = 1 m wurde weggelassen, es wurde also im divergentem Licht gearbeitet. Spaltweite hier 1,5 mm. Die berechneten Schattengrenzen sind durch kurze vertikale Linien in jeder Beugungsfigur markiert.
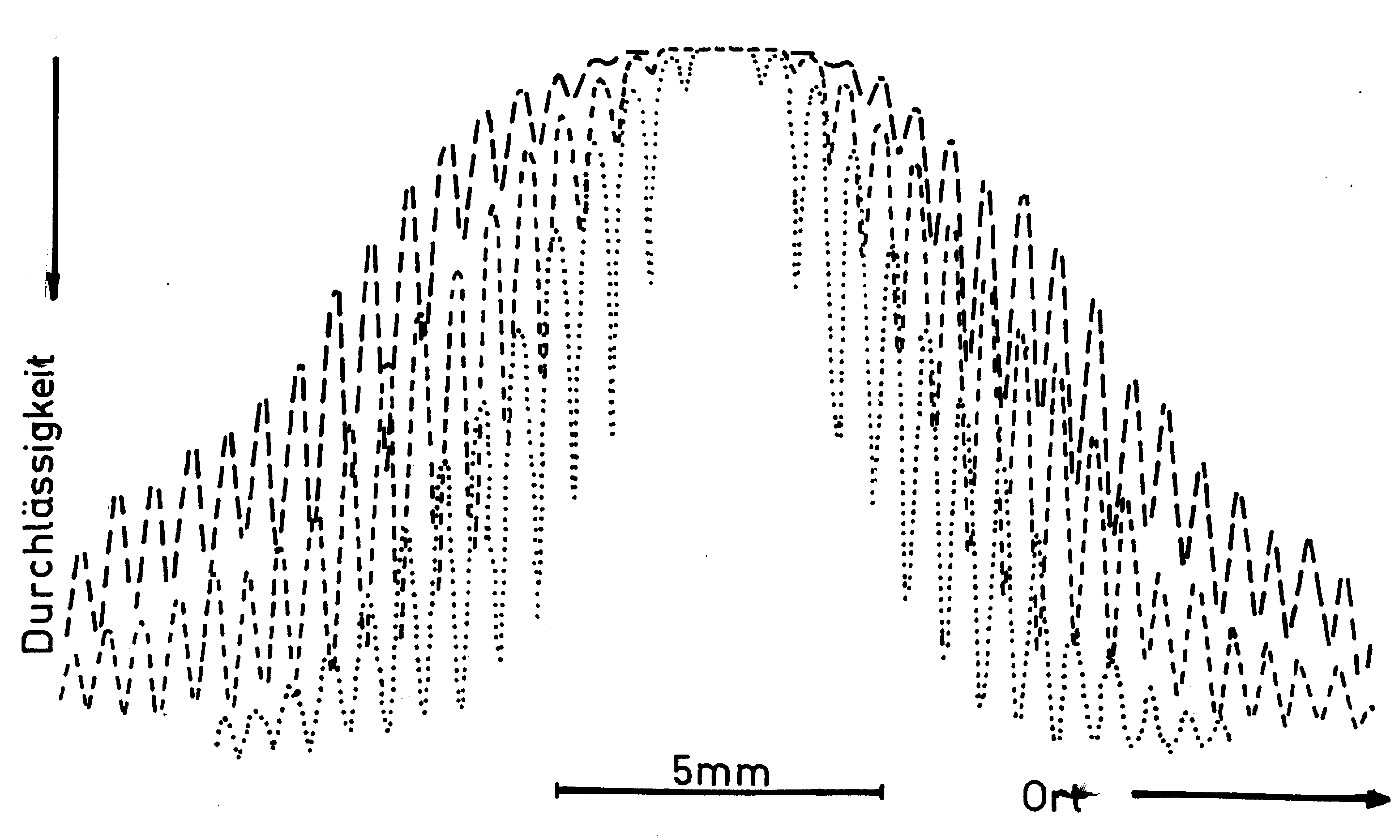
Abb. 3. Photometerkurven von Beugungsfiguren unterschiedlicher Spaltweiten in solchen Entfernungen, daß die Streifenabstände gleich werden, bei gleichen Belichtungszeiten und gleichen Photometerbedingungen. - - Spaltweite 2 mm, --- Spaltweite 1 mm, ... Spaltweite 0,5 mm.
Diskussion
In den Abb. 1 und 2 dominiert noch der Einfluß innerer Beugungsstreifen, Aussagen über den Untergrund lassen sich hier noch nicht treffen. Die Abb. 3 zeigt eindeutig, daß die Breite des Untergrundes mit der Spaltweite wächst, aber hier wurde gleichzeitig die Entfernung geändert, wobei die größere Entfernung bei großen Spaltweiten diesen Einfluß nicht kompensiert. Aus Abb. 3 und den Tabellen 1 bis 4 ist ersichtlich, daß der Untergrund nicht proportional der Entfernung abnimmt, sondern langsamer. Nach Fresnel [5] wachsen die Abstände der Beugungsstreifen der Halbebene bei paralleler Einstrahlung nur proportional der Wurzel der Entfernung. Auch die Abstände der inneren Beugungsstreifen des Spaltes haben diese Entfernungsabhängigkeit bei parallelem Lichteinfall. Also gebeugtes Licht muß auf dem weiteren Weg nicht geradlinig laufen. Es scheint möglich einen Teil des Untergrundes als Rest innerer Streifen anzusehen. Dieser Teil würde bei hinreichender Entfernung in die nullte Ordnung einmünden.
Selbstverständlich bildet ungenügende Monochromasie des Lichtes eine Quelle des Untergrundes wie auch Verunreinigungen an den Kanten. Da die Fraunhofersche Beobachtungsart eine Abbildung des Beleuchtungsspaltes bewirkt, so weisen Beugungsfiguren nach Fraunhoferscher Beobachtungsart einen geringeren Untergrund auf. Da hier in der Brennebene keine inneren Beugungsstreifen auftreten, wird der Untergrund durch die Abbildung reduziert.
Literatur
[1] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Arbeit 4.
[2] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. London 1704; Opera quae exstant omnis, Tom IV. London 1782; Reprint, Bruxelles 1966; Optik II + III, Übers. W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmann, Leipzig 1898; Neuauflage Bd. 96/97, Vieweg, Braunschweig 1983; Optique, Trac. J. P. Marat 1787; Bourgois , Paris 1989.
[3] Wie [1], Arbeit 1.
[4] Wie [1], Arbeit 2.
[5] A. J. Fresnel, Ouvres Complétes 1. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.
© 2006 by tediamedia • info@gebeugtes-licht.de