
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Überlagerung von Interferenz und Beugung
Es wird in einem Mach-Zehender Interferometer gezeigt, daß sich die Beugungsfigur in einer Halbebene nicht ungestört mit der Interferenzfigur überlagert. Das wird darauf zurückgeführt, daß Photonen der Beugungsfigur der Halbebene nicht geradlinig laufen. Das Gleiche wird mit Newtonschen Ringen gezeigt, wo sich ebenfalls Beugung und Interferenz nicht ungestört überlagern. Bei der Streuung hingegen konnte die Überlagerung nicht geprüft werden, es wird diskutiert, warum in einer normalen Interferenzapparatur die gewohnte Streufigur nicht entstehen kann.
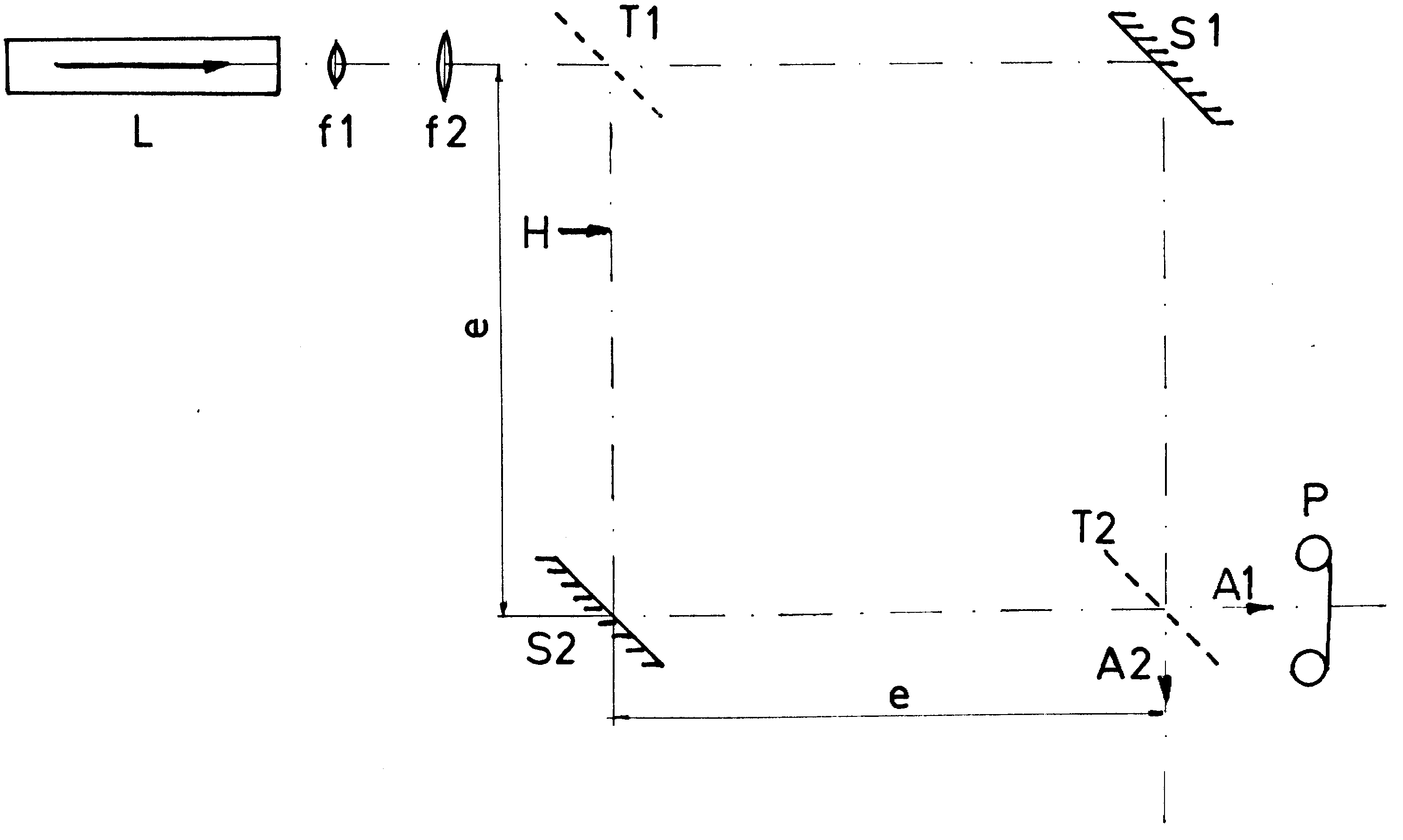
Abb. 1: Mach-Zehender Interferometer (Leybold Didaktik). L - He-Ne-Laser; f1, f2 - Linsen zur Strahlungsaufweitung, parallel eingestellt; T1, T2 -Strahlungsteiler; H - bei einigen Aufnahmen Ort der Halbebene oder der Streuplatte; e - Entfernungen 16,5 cm; S1, S2 - Spiegel; A1, A2 - Ausgänge, wie Positiv und Negativ; P - Kamerakörper einer einäugigen Spiegelreflexkamera.

Abb. 2. Interferenzfigur des Interferometers nach Abb. 1.
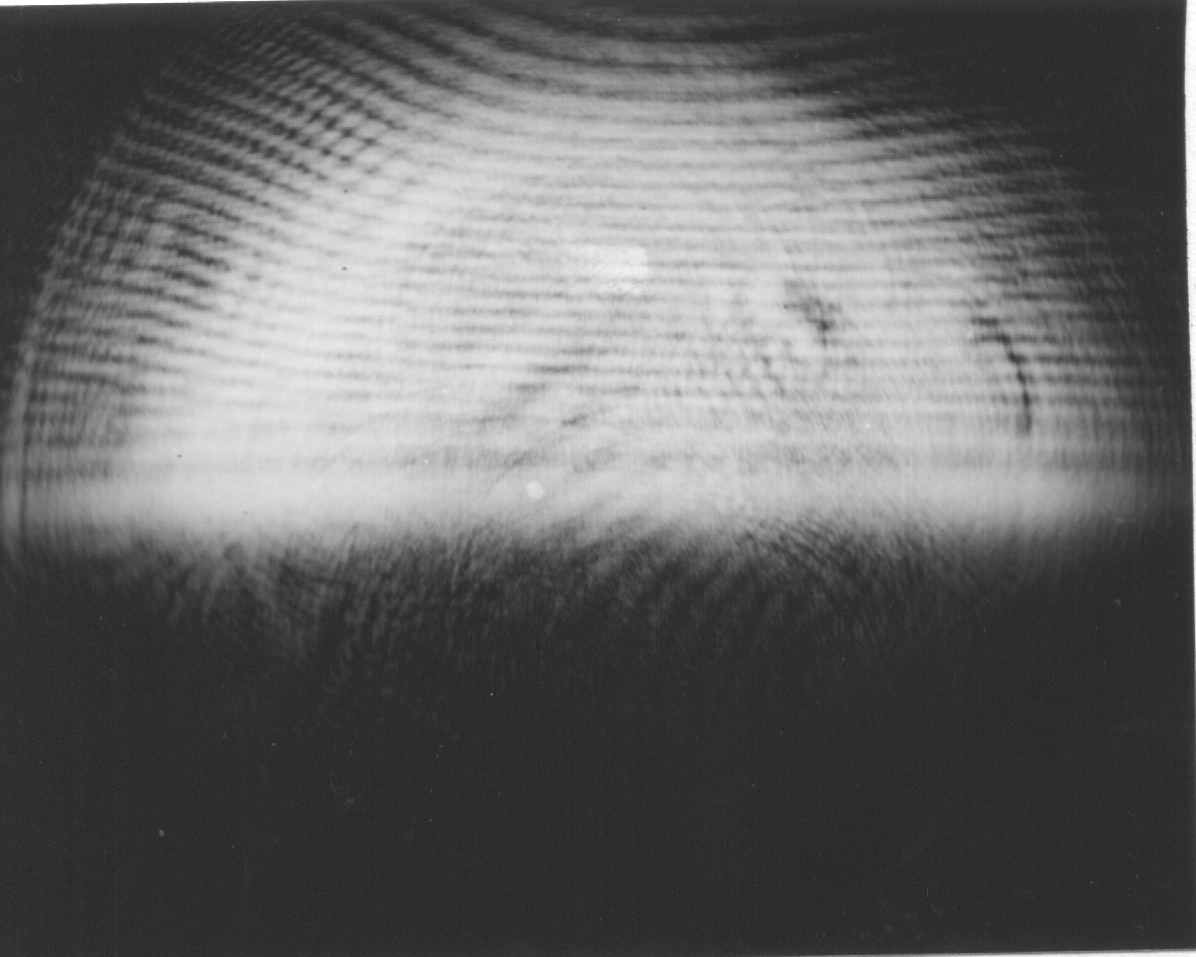
Abb. 3. Beugungsfigur einer Halbebene in H mit abgedecktem anderen Lichtweg.

Abb. 4. Überlagerung der Beugungs- und Interferenzerscheinungen.
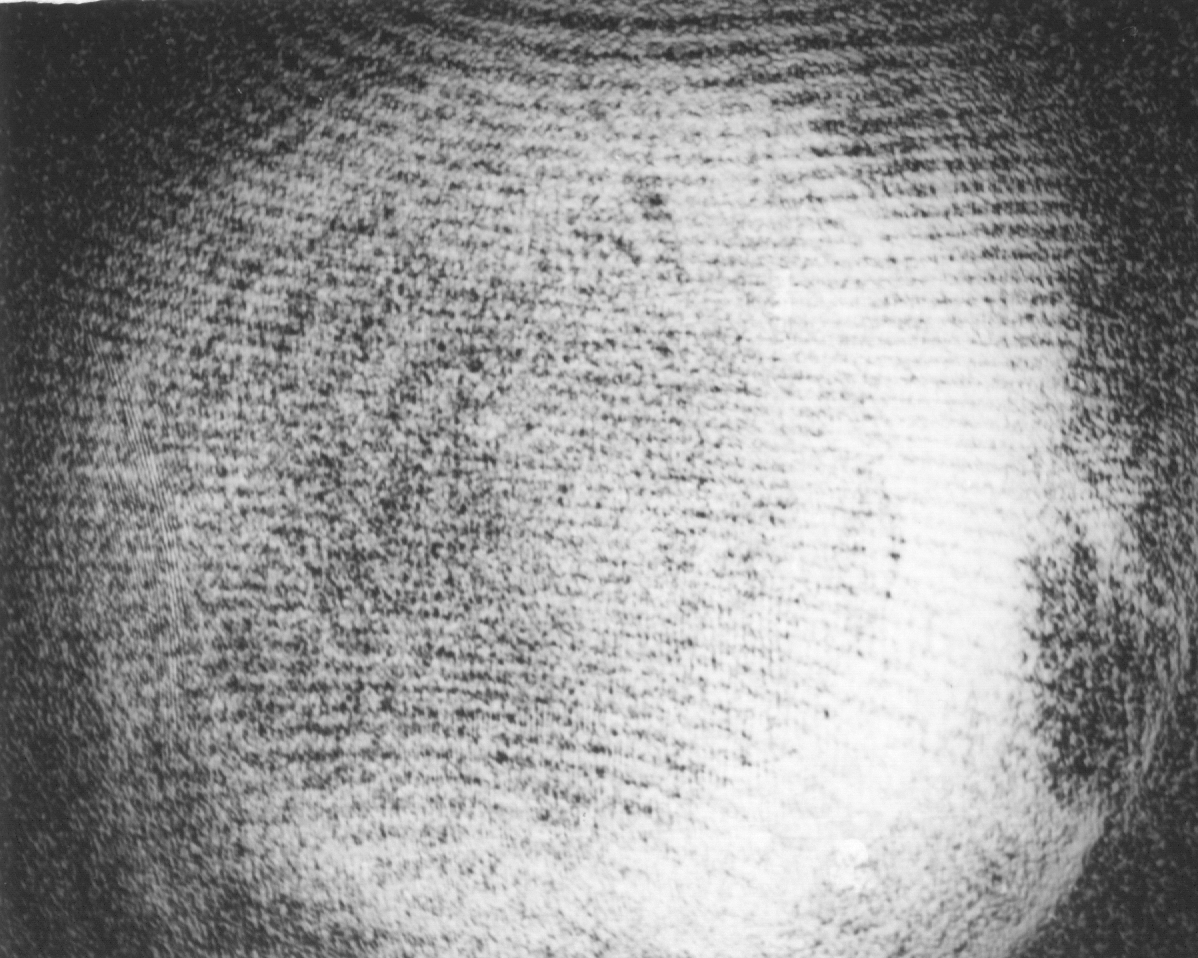
Abb. 5. Ungestörte Interferenzfigur mit einem klaren Objektglas in H der Abb. 1. Neu justiert für Abb. 6 bis 8.
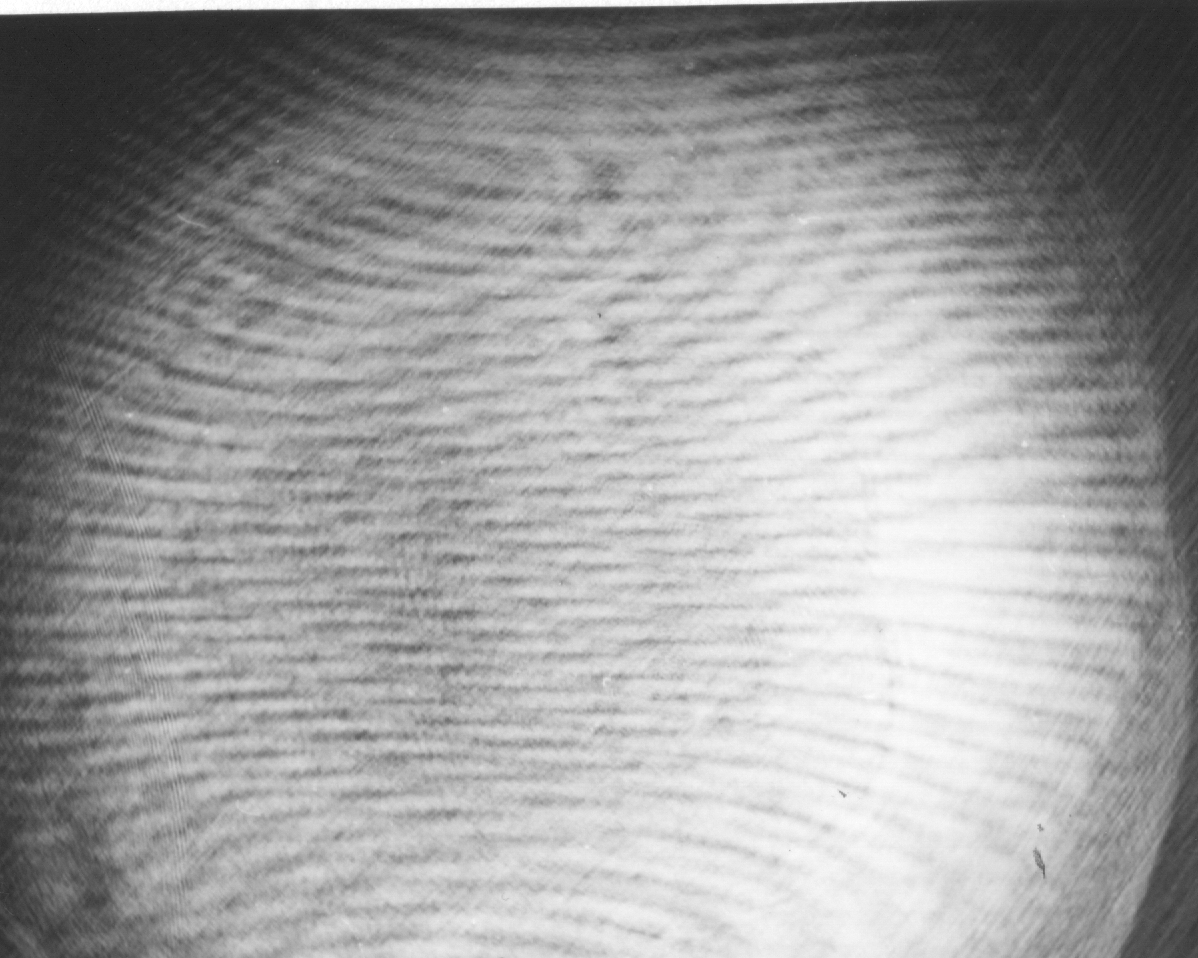
Abb. 6. Streufigur mit Bärlappsporen auf der Objektglas in H, der andere Lichtweg war abgedeckt.

Abb. 7. Gesamtergebnis mit Streufigur überlagert von der Interferenzfigur.
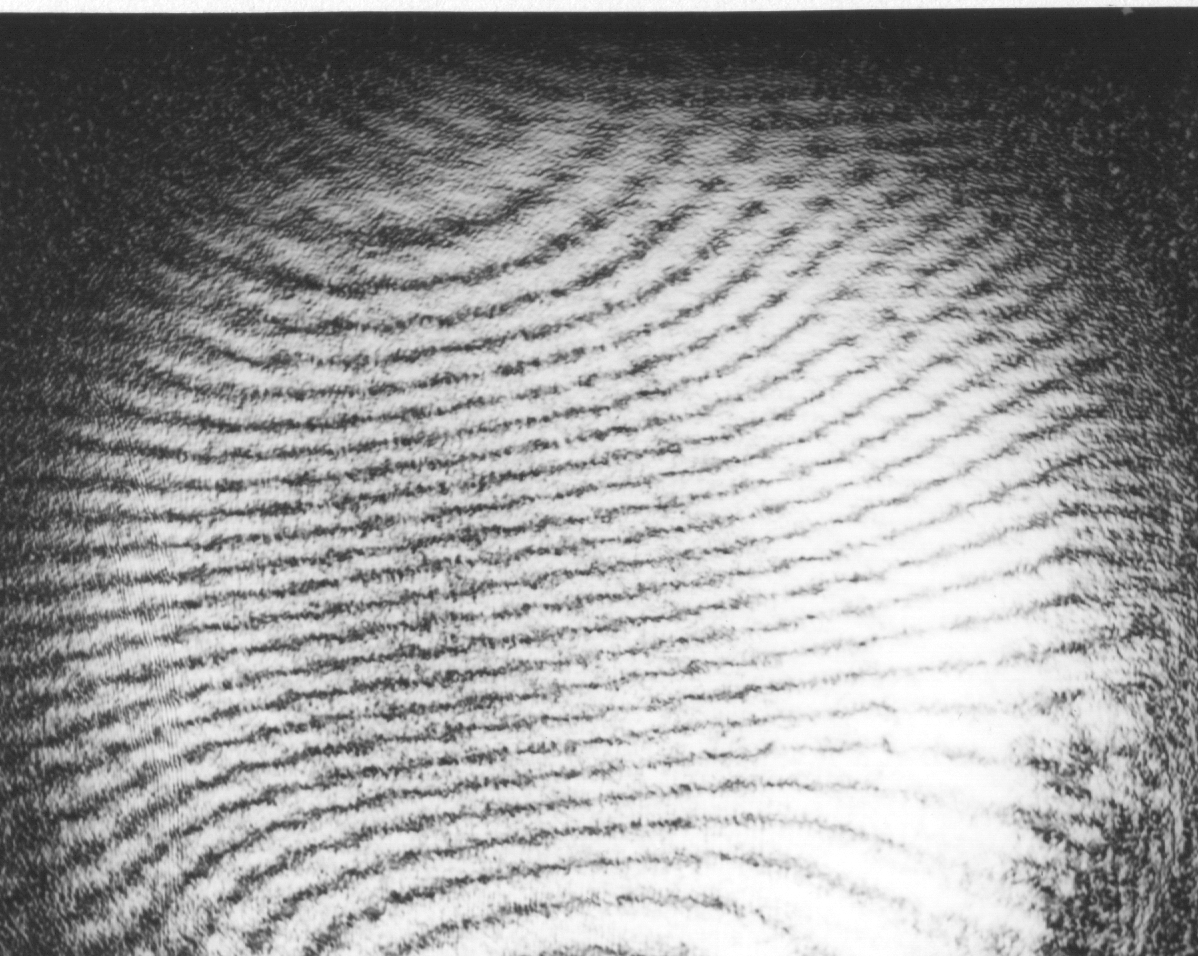
Abb. 8. Wie Abb. 7, aber das Objektglas mit dem Bärlappsporen zusätzlich bewegt
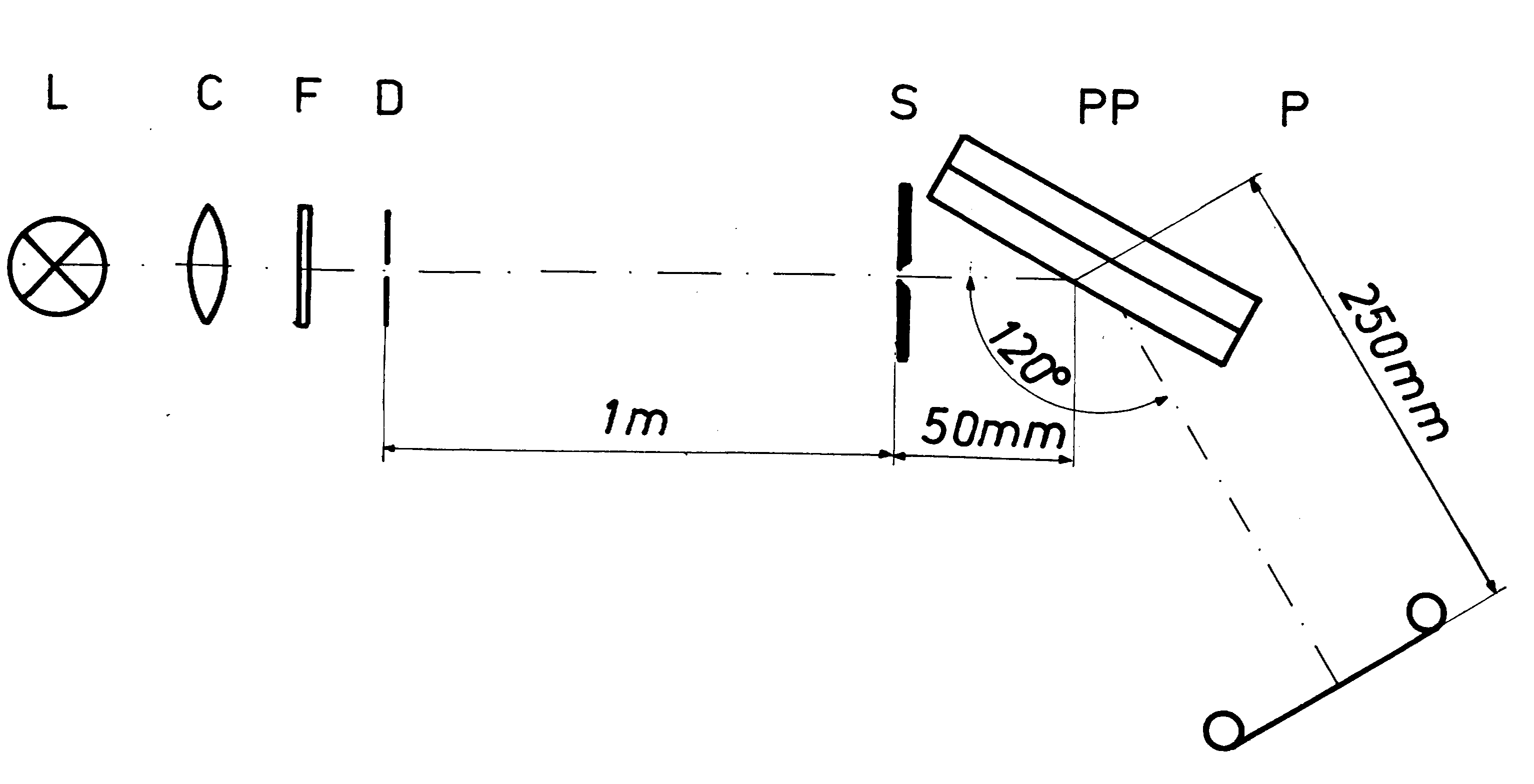
Abb. 9. Experimentelle Anordnung zur Untersuchung der Newtonschen Ringe bei Beleuchtung mit Beugungsstreifen in Reflexionsstellung. L - Lichtquelle, eine Quecksilber-Höchstdrucklampe HBO 100; C - Kondensor; F - Grünfilter; D - Kreisblende Ø 0,1 mm; S - veränderlicher Spalt; PP - Planplatten, die Newtonsche Ringe zeigen; P - Photofilm.

Abb. 10. Teile Newtonscher Ringe nach Abb. 9, beleuchtet bei einer Spaltweite von S mit 2 mm. Pfeile - vgl. Text.
Diskussion der Streuexperimente
Für die Streuung an unregelmäßigen Teilchen wird üblicherweise Bärlappsporen benutzt, wie dies z.B. bei Pohl [11] mit eingestaubten Spiegeln und regellosen Kreisöffnungen beschrieben wurde. Die Sichtbarkeit der dort beschriebenen Streufigur setzt voraus, daß nur eine kleine Fläche beleuchtet und diese auf eine große Fläche projiziert wird. In einer üblichen Interferenzapparatur ist also diese Streufigur nicht zu erreichen, sondern wie in Abb. 6 sind nur die Streuteilchen als Punkte zu sehen. Nun kann man Interferenzen auch mit divergentem Licht zeigen, das erfordert aber eine spezielle größere Apparatur, wo das Licht bis H konvergent geführt wird und dann ab H mit Streuplatte divergent. Das könnte also versucht werden.
Dann ist noch Laue [12] zu zitieren, der bei unregelmäßig angeordneten Streuteilchen über ein Versagen der klassischen Wellentheorie berichtete. Er berichtete auch von radialen Fasern, die der Theorie nicht entsprachen, wie auch Nieke [6] über sternförmige Streufiguren. Laue [13] schrieb: ,,... denn Versuch und Theorie sind an dieser Stelle bisher aneinander vorübergegangen, ohne voneinander recht Kenntnis zu nehmen." Er stellt in dieser Arbeit die Differenzen gegeneinander ohne sie zu lösen.
Die sog. Wellenoptik versagt nach Laue bei Streufiguren, aber auch bei der Beugung bei Berücksichtigung der Newtonschen Beugungsexperimente (Nieke [6] und [14]), auch wenn für Spezialfälle Fresnel mit Hilfe des Fourier-Theorems Lösungen angeben konnte. Mit dem Fourier-Theorem kann man jede stückweise monotone Funktion näherungsweise darstellen, notfalls mit Hilfe eines nur wegen der Abweichung der Wellentheorie von experimentellen Ergebnissen eingeführten Phasensprunges. Laue [12] schrieb: ,,Wir sehen darin ein Versagen der klassischen Wellentheorie, die sich doch sonst bei allen Interferenz- und Beugungserscheinungen so vortrefflich bewährt hat." Hier berücksichtigte Laue nur die mathematisch formale Anwendung des Fourier-Theorems in Spezialfällen und nicht die Newtonschen Beugungsexperimente ([8] Buch III Beobachtung 5 und 10, und Nieke [14]). Hier wird Laue nirgends zitiert, genau wie Laue [15] in seinem Handbuchartikel über die Beugung Newtons Beugungsexperimente nicht zitierte.
Literatur
[1] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Arbeit 5.[2] A. Fresnel, Oevre Complétes 1. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.
[3] W. M. Honig, In: Hrsg. W. M. Honig, D. W. Kraft, E. Panarella: Quantum Uncertainties. Nato AST Series B Vol 162, Plenum Press NY, London 1987, S. 97: Summary of de Martini's Paper.
[4] H. Nieke, Exp. Techn. Phys. 31. (1983) 53.
[5] Wie [1], Arbeit 4.
[6] Wie [1], Arbeit 2
[7] Wie [1], Arbeit 3
[8] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and Co- lours of Light. 1704; Opera quae exstant omnis, Tom IV. London 1782; Reprint, Bruxelles 1966; Optik II + III, Übers. W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmann, Leipzig 1898; Neuauflage Bd. 96/97, Vieweg, Braunschweig 1983. Optique, Trac. J. P. Marat 1787; Bourgois; Paris 1989.
[9] L. de Broglie, La Physique quantique restera-t-elle indéterministe? Gauthier-Villars Paris 1953. Phys. Bl. 19 (1953) 488, 541.
[10] E. Mach, Die Prinzipien der physikalischen Optik. Barth, Leipzig 1921
[11] R. W. Pohl, Optik. 8. Aufl. 1948 Springer, Berlin, Göttingen, Heidelberg S. 79 u. 107.
[12] M. v. Laue, Ber. Dtsch. Phys. Ges. 19 (1917) 19.
[13] M. v. Laue, Sitzungsber. Akad. Wiss. Berlin 1914 XLVII S. 1144.
[14] Wie [1], Arbeit 1
[15] M. v. Laue, In: Handbuch der Experimentalphysik Bd 18. Akad. Verlagsges. Leipzig 1928.
© 2006 by tediamedia • info@gebeugtes-licht.de