
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Faradays elektro-tonische Zustände
Es wird experimentell gezeigt, daß sich die Feldlinien von stromdurchflossenen Spulen oder Dauermagneten nicht nur zwischen diesen im Abstoßungs- oder Anziehungsfall ändern, sondern auch an den äußeren Enden werden die Feldlinien verlagert, bei Anziehung nach innen und bei Abstoßung nach außen. Die Verschiebung an den äußeren Enden ist bei kurzen Spulen leicht nachzuweisen, die Verlagerungen sind abhängig vom Abstand der Magnete, bei langen Spulen oder Magneten ist dieser Effekt nur angedeutet. Mit dieser Verlagerung der Feldlinien als Kraftlinien könnte die Wirkung der Kraft begründet werden, allerdings weiß man nicht was das ist, 'ein Feld'.
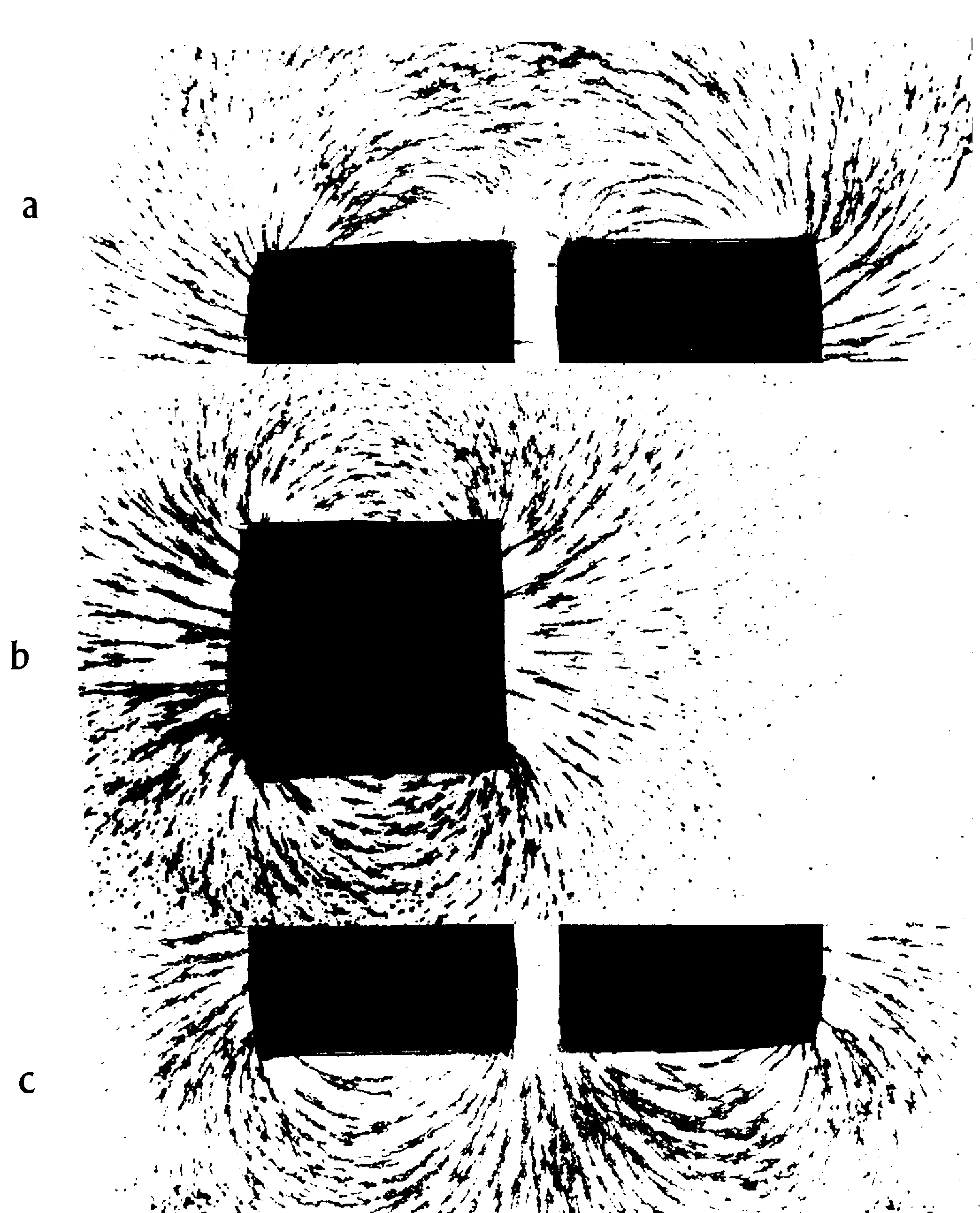
Abb. 1 Feldlinienbilder von Spulen im Abstand von 12,5 mm.
a: Feldlinienbild im Fall der Anziehung (oberer Teil),
b: Feldlinienbild einer Spule,
c: Feldlinenbild im Fall der Abstoßung (unterer Teil)

Abb. 2. Feldlinienbilder von Ringströmen mit einem Abstand von 2 mm.
a: Feldlinienbild im Fall der Anziehung (oberer Teil),
b: Feldlinienbild eines Ringbündels,
c: Feldlinienbild im Fall der Abstoßung (unterer Teil).
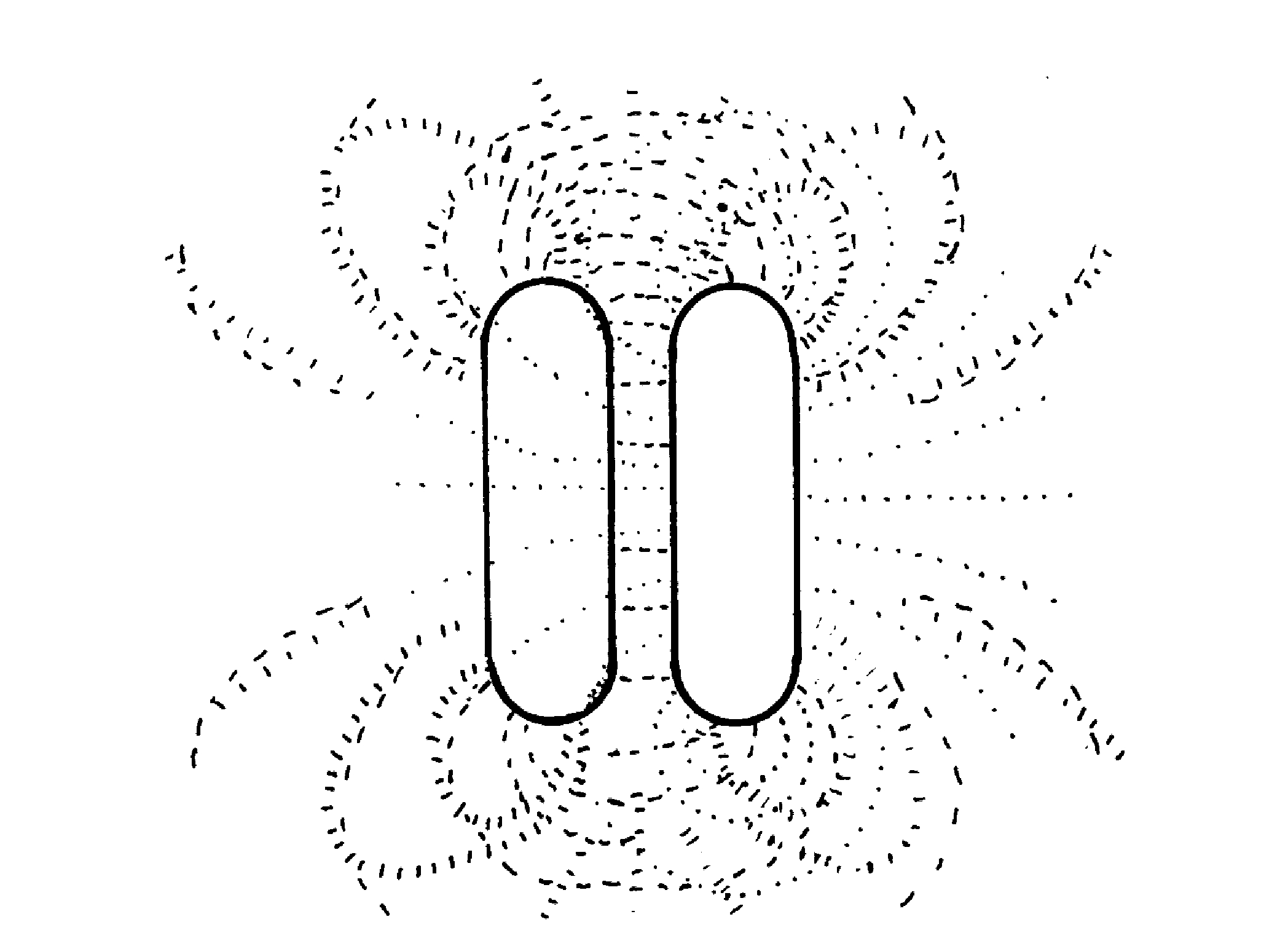
Abb. 3. Ausgewählte Feldlinien von Ringbündeln im Abstand von 5 mm.
- - - Fall der Anziehung,
. . . nur eines Ringbündels,
| | | Fall der Abstoßung.

Abb. 4. Feldlinienbilder von Dauermagneten mit dem Abstand von 2 mm.
a: Fall der Anziehung (oberer Teil),
b: Feldlinienbild eines Magneten,
c: Fall der Abstoßung (unterer Teil).
Diskussion
Diese Experimente zeigen, daß die gesamten Feldlinien sich bei einer Umpolung ver-lagern und nicht nur zwischen den beiden Spulen oder Magneten, sondern auch an den äußeren Enden.Dabei ist zu bedenken, daß die Feldlinien sich aus der Summation der Kreisströme bzw. der Elementarmagnete ergeben, daher ist dieser Effekt geringer bei langen Spulen oder Magneten. Wie schon oben bemerkt, hängt die Richtung der Feldlinien nicht merklich von der Stromstärke oder der Magnetisierung ab, wohl aber vom Abstand der Magnete auch an den äußeren Enden. Oder wenn man von der Idealisierung ausgeht, daß die Feldlinien von einem Pol ausgehen und zum anderen laufen, so läuft im Fall der Abstoßung das Feld hinter den äußeren Polen zurück. Im Fall der Anziehung läuft das Feld zu einem Gebiet vor den inneren Polen.
Aus dieser Erscheinung der Verlagerung der Feldlinien, oder der von ihnen gebildeten Schläuche, etwa ihres Schwerpunktes (oder entsprechend der Abstände modifizierten Schwerpunkte) als Kraftlinien entsprechend der Abstände zweier Spulen oder Magnete, könnte man eine Kraftwirkung begründen, wenn noch die Feldstärke berücksichtigt wird. Maxwell [5] vermutete Druckwirkung durch die Zentrifugalkraft der Wirbel des Äthers.
Daß sich im Fall normalleitender Spulen die magnetischen Momente der Elektronen ausrichten, ist bei den Stoßprozessen, denen sie unterworfen sind, nicht anzunehmen, es bilden sich also nur magnetische Blätter. Anders bei zwei supraleitenden Spulen, hier ist eine Ausrichtung der magnetischen Momente der kreisenden Elektronen denkbar, es bildet sich nach Nieke [9] je ein magnetisches Moment-Blatt.
Hoppe [6] berichtete, daß Gilbert den Magnetismus als eingegebene Wirbelkraft betrachtete und nur die Anziehung als Streben nach Vereinigung annahm, die Abstoßung diskutierte er als Drehung. Damit hatte die Gravitation keine Sonderstellung. Sicher hat dies Faraday aufgegeben, um die Analogie zur elektrischen Ladung zu wahren.
Die Beschreibung der obigen Experimente als Verlagerung der Kraftlinien gibt die Möglichkeit einer Beschreibung, eine wirkliche Begründung scheitert daran, daß wir nicht wissen, was ,ein Feld' ist. Die obigen Experimente geben dazu keinen zusätzlich Aufschluß. Nach Faraday [1] ist das Feld ein Zustand der Spannung, nach Maxwell [4] ein schönes Bild, nach Einstein [7] eine konstruktive Spekulation; wenn paarweise abgelöst: nach Hertz elektromagnetische Strahlung, die nach Nieke [10] in selbstwechselwirkende Photonen zerfällt, ....
Literatur
[1] M. Faraday, Philosophical Transactions 173 (1832) 91, Art. 60; Pogg. Ann. Phys. u. Chem. XXV (1832) 91, Zitat S. 110; Experimental-Untersuchungen über Elektrizität. Ostwald's Klassiker Nr. 31, Engel mann, Leipzig 1896, Art. 60 S. 19.
[2] J. C. Maxwell, Transact. Cambr. Phil. Soc. 10 (1355/6) 27; Scientific Papers, Vol 1, quotation p. 187; Über Faradays Kraftlinien. Ostwald's Klassiker Nr.69, Engelmann, Leipzig 1912. Zitat S. 44.
[3] wie [2] Scientific Papers p. 137-8; - Nr. 69, S. 46.
[4] J. C. Maxwell, Phil. Mag, Ser. 4, 21, (1861) 161;
Scientific Papers, Vol. 1. quotation p. 451-452; Uber physikalische Kraftlinien. Ostwald's Klassiker Nr. 102, Engelmann, Leipzig 1898, Zitat S. 4.
[5] Wie [4] Scientific Papers quotation p. 468 and 489; Nr. 102, S. 25 und 54
[6] M. L. Hoppe, Die Abhängigkeit der Wirbeltheorie des Descartes von W. Hilberts Leh- re vom Magnetismus. Diss. Halle 1914.
[7] A. Einstein, The Journal of the Franklin Institute 221 Nr. 3 (1936); Aus meinen späten Jahren. D. Verl.-Anst. Stuttgart 1979, S. 82-84; Out of my Later Years. Phil. Lit. New York 1950.
[8] Wie [7] Botschaft Gedenkfeier 100. Geburtstag H. A. Lorentz (1953); Aus meinen späten Jahren S. 228.
[9] H. Nieke, Newtons Beugungsexprimente und ihre Weiterführung. Arbeit 17.
[10] Wie [9], Arbeit 12
© 2006 by tediamedia • info@gebeugtes-licht.de