
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Beugung von Licht an Spalt und Hindernis
Eingangs wird gezeigt, daß sich die Beugungsfigur der Halbebene aufbaut, und erst in einer Entfernung von ~ 105 λ (bei paralleler Einstrahlung) tritt die bekannte Form auf. In einer Schlierenapparatur nach Abbe liefern Spalt und Hindernis gleicher Abmessung als Bilder beidseitig jedes Kantenbildes einen Doppelstreifen (< 0,1 mm breit) mit einem schmalen dunklen Zwischenstreifen. Gebeugtes Licht scheint also aus analogen Gebieten zu kommen. Ohne Schlierenapparatur entstehen kantensymmetrisch vertauscht (nur in Spezialfällen gleich) die gleichen Beugungsfiguren mit inneren und äußeren Beugungsstreifen. Generelle Bemerkungen über innere und äußere Beugungsstreifen ergänzen die Arbeit.
Experimente und Abbildungen
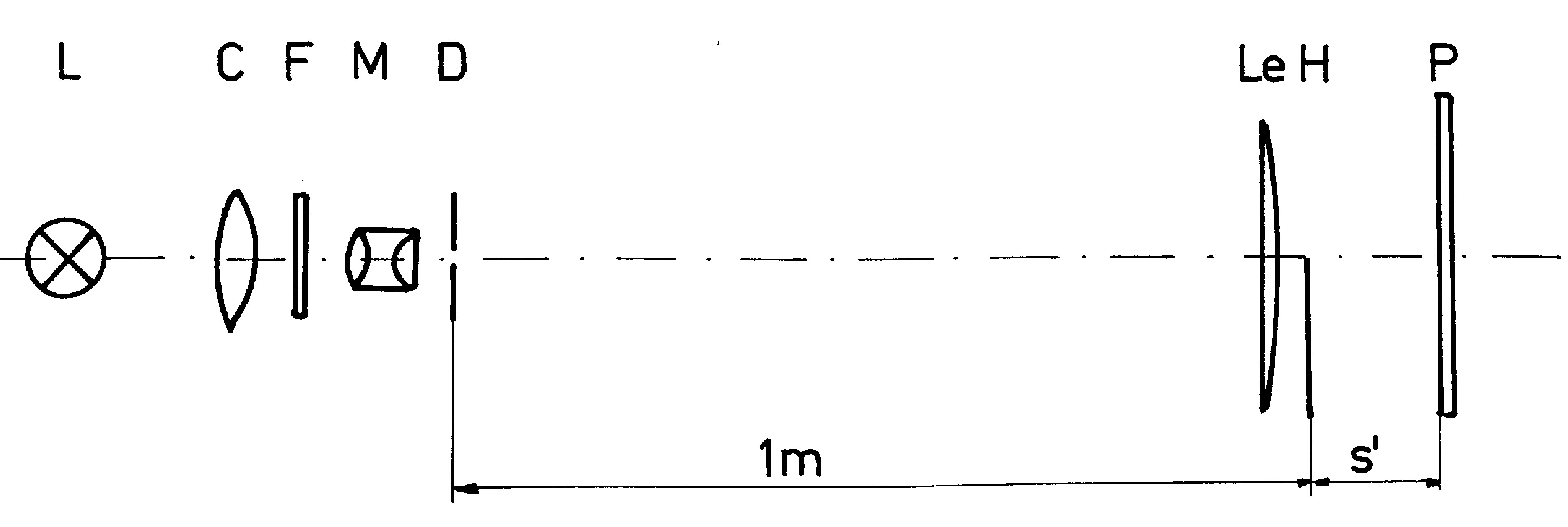
Abb. 1. Experimentelle Anordnung zur Aufnahme der Beugungsfigur der Halbebene in sehr kurzen Entfernungen. L - Lichtquelle, eine Hg-Höchstdrucklampe HBO 100; C - Kondensor; F - Grünfilter; M - Mikroskopobjektiv; D - Kreisblende, eine Spinndüse 50 mm; Le - Linse, f' = 1 m; H- Halbebene; s = 1 m; s' - Entfernung H bis P; P - Photofilm.
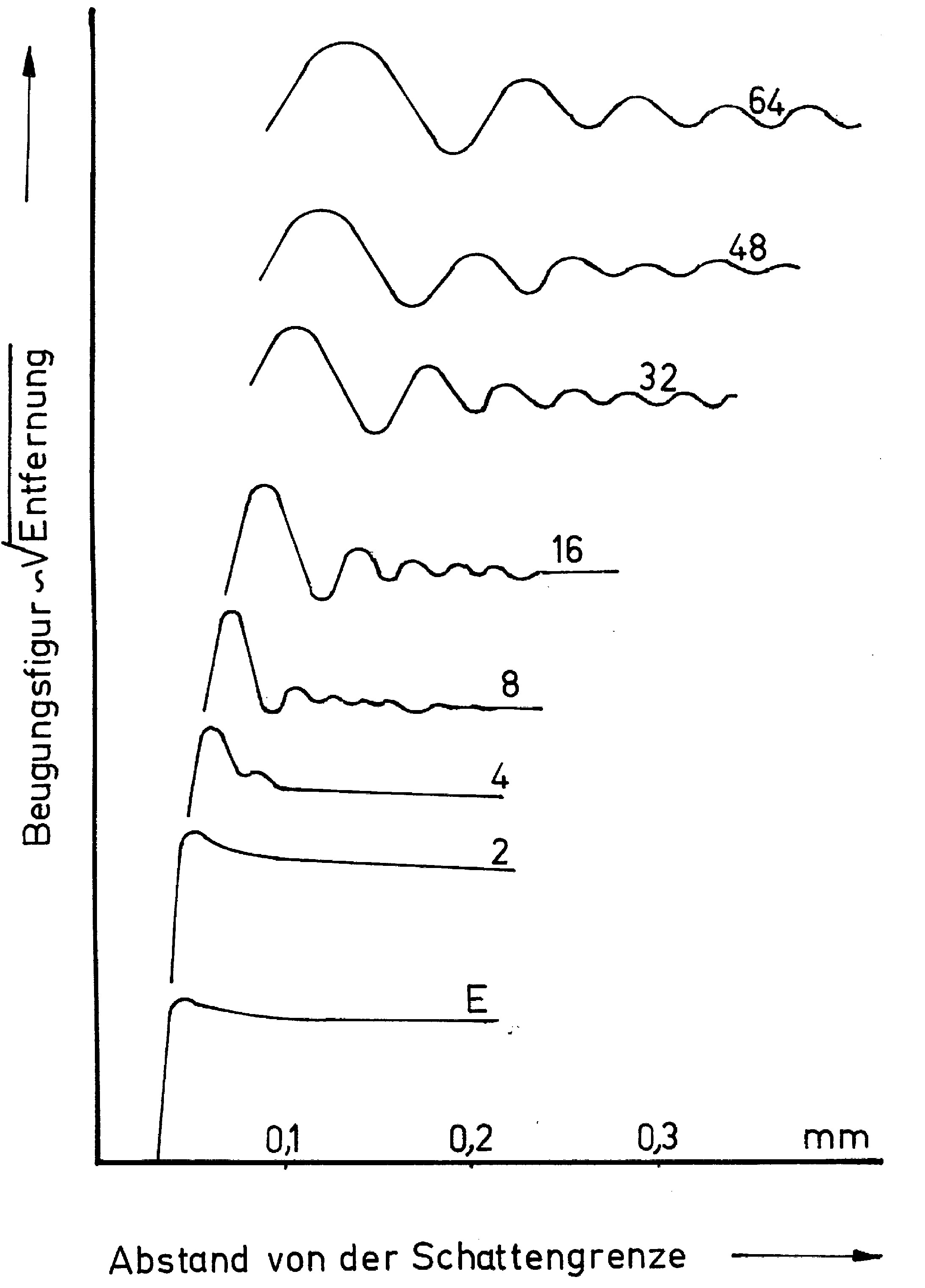
Abb. 2. Photometerkurven der Beugungsfigur der Halbebene in Abhängigkeit der Entfernung s' nach Abb. 1. In der Ordinate wurden die Photometerkurven so verschoben, daß jede etwa an der Stelle aufgetragen ist, die der Wurzel aus der Entfernung s' entspricht. Die Zahlen bedeuten s' in mm, E - Film dicht hinter der Kante.


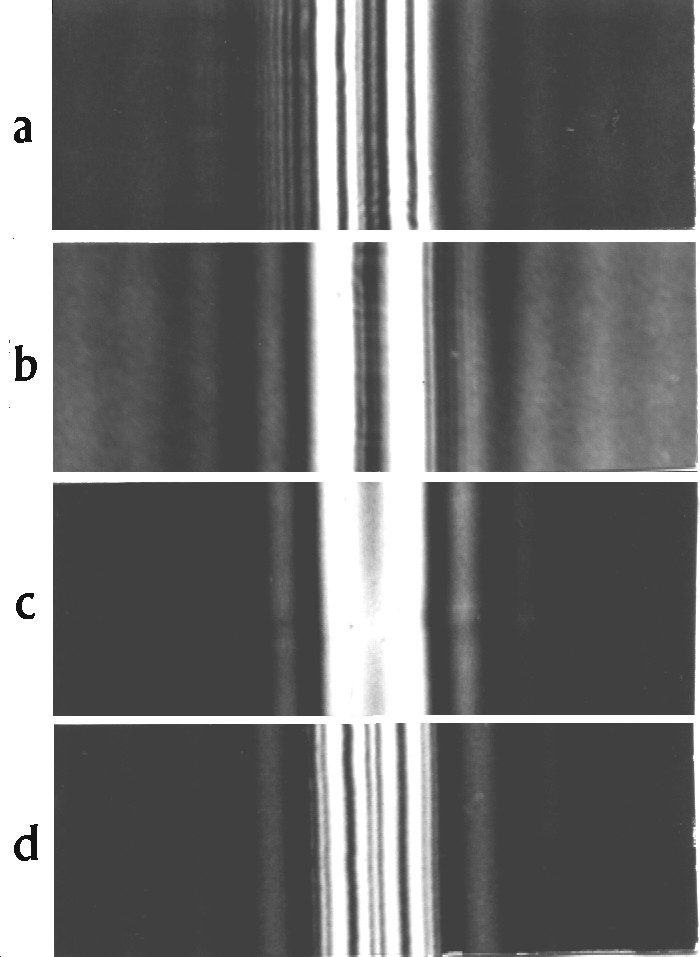
a: Draht-Bild 2 mm vor der Überkreuzungsebene,
b: Draht-Bild in der Überkreuzungsebene
c: Spalt-Bild in der Überkreuzungsebene
d: Spalt-Bild 2 mm hinter der Überkreuzungsebene.
Abb. 3(links). Bild von Hindernis und Spalt in einer Abbeschen Schlierenapparatur nach Nieke [5] dort Abb. 1. Draht und Spalt 0,5 mm, a' / a = -4 und nachvergrößert.
Abb. 4(mitte). Bild von Hindernis und Spalt der Abmessung 0,2 mm in der Schlierenapparatur, a. . .d wie Abb. 3.
Abb., 5(rechts). Bild von Hindernis und Spalt der Abmessung 0,1 mm in der Schlierenapparatur, a. . .d wie Abb. 3

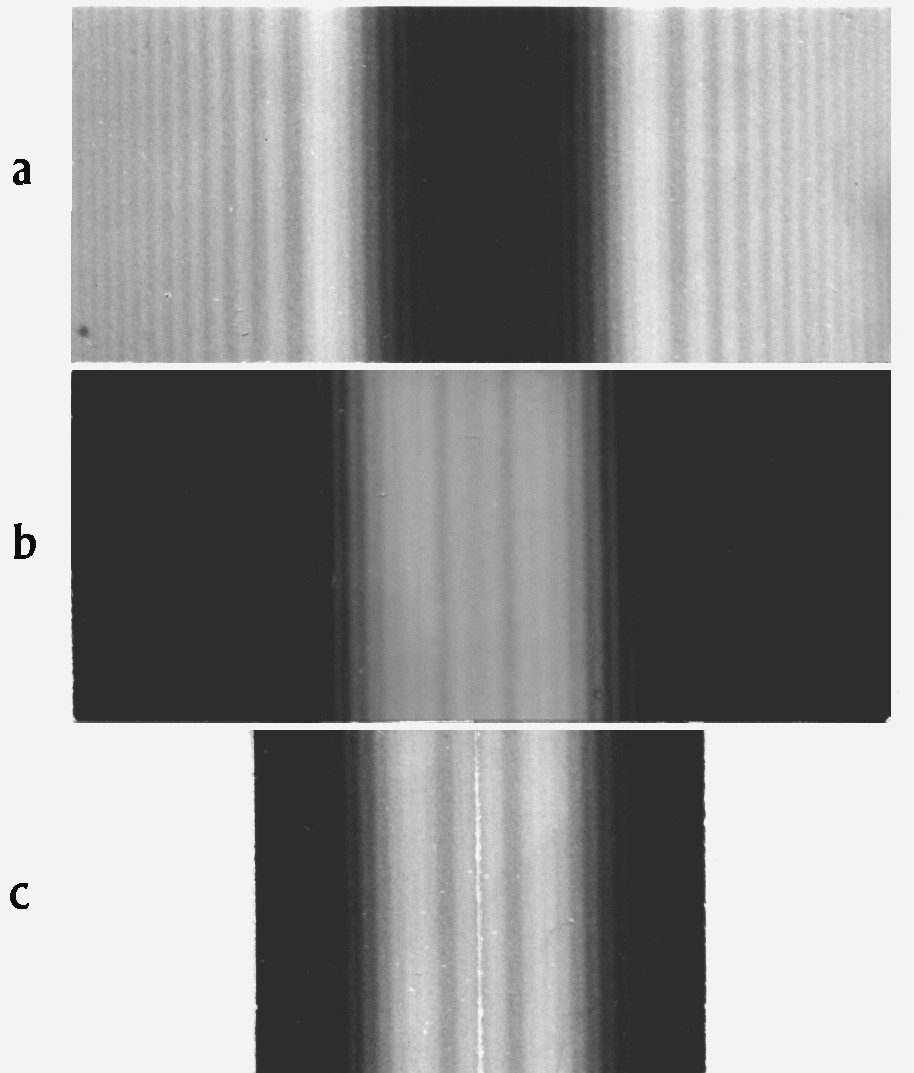
Abb. 6. Beugungsfigur von Hindernis und Spalt in 0,1 m Entfernung. Ohne Schlierenapparatur in Fresnelscher Beobachtungsart mit parallel einfallendem Licht. a: Draht f 1,5 mm,, b: Spalt 1,5 mm,. c: Beugungsfigur a in der Mitte zerschnitten und spiegelbildlich aufgeklebt.
Abb. 7. Wie Abb. 6, aber in 0,3 m Entfernung. Die äußeren Beugungsstreifen des Hindernisses und die inneren des Spaltes entsprechen
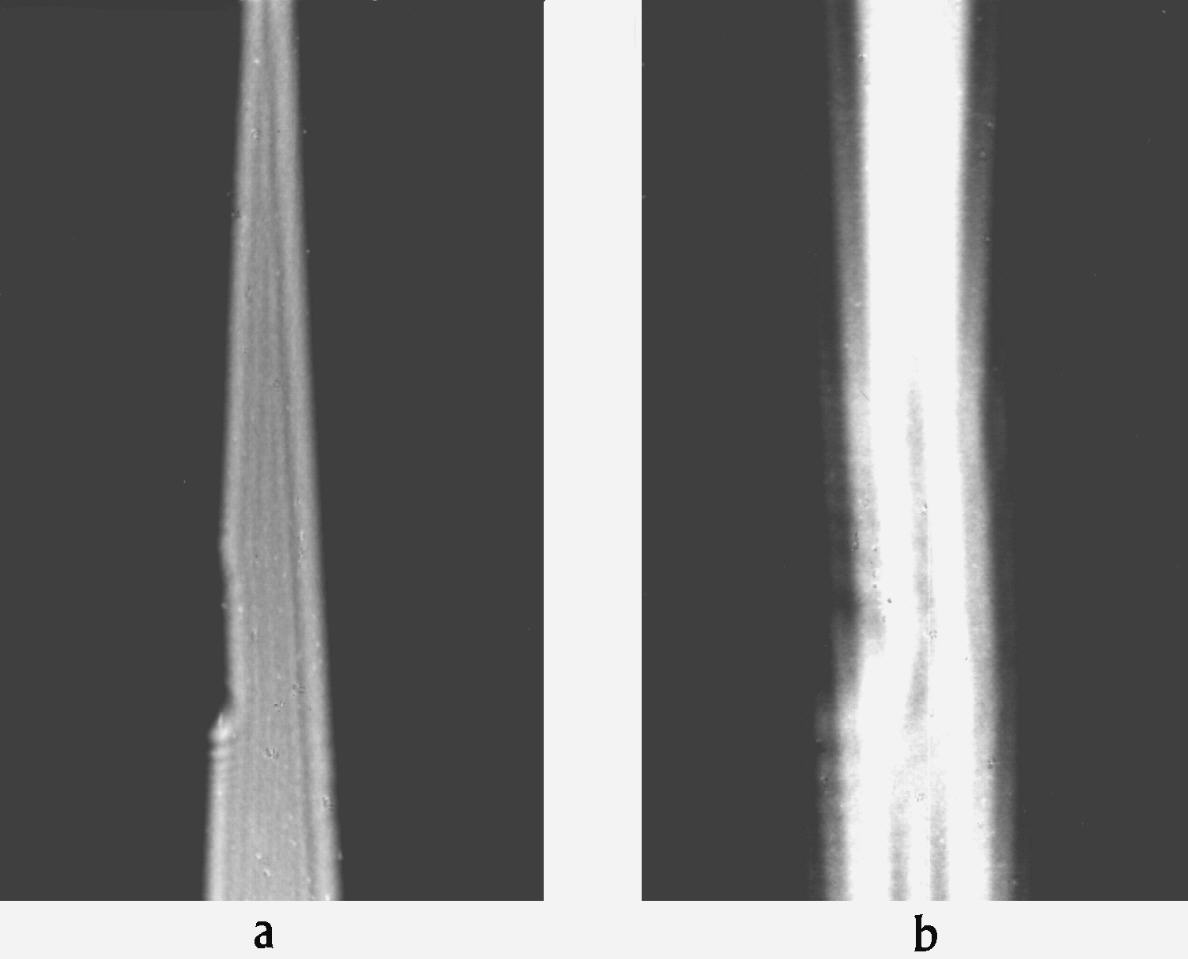
Abb. 8. Beugung am Dreieckspalt mit Schnitzel. Eine Hg-Höchstdrucklampe mit Grünfilter wurde auf eine Öffnung f 0,05 mm abgebildet. In 1 m Entfernung stand ein Dreieckspalt 0...3 mm mit einem Kupferschnitzel an einer Kante. (Also divergent beleuchtet.) a: Beugungsfigur in 0,1 m Entfernung, b: Beugungsfigur in 0,5 m Entfernung.
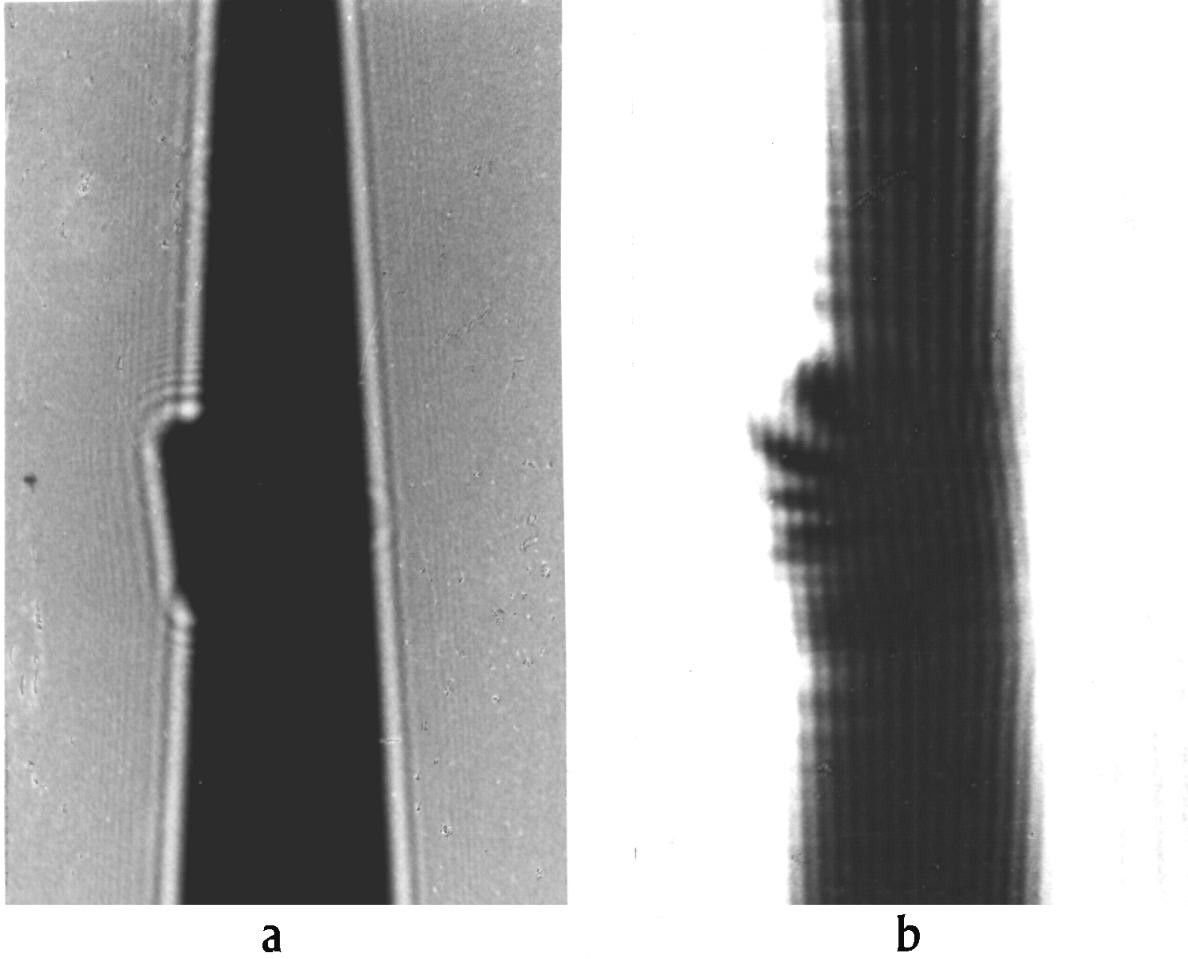
Abb. 9. Beugung mit Dreieckhindernis mit Schnitzel. Wie Abb. 8, aber statt Dreieckspalt - Dreieckhindernis.
Diskussion
Als Mangel in den bisherigen Beschreibungen über die Beugung an komplementären Schirmen, findet man die Tatsache, daß bewußt oder unbewußt eine Diskussion über innere und äußere Beugungsstreifen vermieden wurde. Das geschah, weil man den Übergang innerer zu äußeren Beugungsstreifen am Spalt nicht begründen konnte. Hier wies Nieke [10] darauf hin, daß die Begründung: ,,Hinreichend auseinander gerückte Kanten müssen die Beugungsfigur der Halbebene liefern, nicht stichhaltig ist, sondern es muß erklärt werden, warum bei gleicher Spaltweite in kurzen Entfernungen innere und bei größeren äußere Beugungsstreifen auftreten. Nur mit der Fraunhoferschen Beobachtungsart scheint diese Schwierigkeit behoben, denn da treten (in der Brennebene) nur äußere Beugungsstreifen auf. Bei einer wirklichen Beschreibung dürfen die Augen nicht vor Schwierigkeiten verschlossen werden, dafür ergibt sich ein übersichtliches Bild über das Babinetsche Theorem, wenn die Kantensymmetrie der Beugungserscheinungen betont wird. Dann findet man in Spezialfällen eine Übereinstimmung, wenn die Zentralfigur ausgenommen wird. Die Versuche mit Schnitzel an den Spaltkanten zeigen, daß man auch im Spalt oder am Hindernis experimentieren kann (auch wenn das Born und Biem [14] in Abrede stellten), aber dann muß zwischen inneren und äußeren Beugungsstreifen am Spalt oder Hindernis unterschieden werden. Bei inneren Streifen am Spalt oder äußeren am Hindernis, also in kurzen Entfernungen, wirkt das Schnitzel nur auf die Beugungsfigur der Kante, an der es angebracht wurde. Bei größeren Entfernungen, wenn die äußeren Beugungsstreifen des Spaltes und die inneren des Hindernis auftreten, dann wirkt das Schnitzel auf die Beugungsfigur insgesamt. Lohmann u. Sinzinger [15] untersuchten das Babinetsche Prinzip, wenn nur ein Teil der Computerholographie komplementär vertauscht wurde. Sie bezeichneten dies als lokalen Babinet Effekt. Das Prinzip der kantensymmetrischen Vertauschung der Beugungsfigur kann hier nicht zum Ausdruck kommen, denn sie vergleichen nur mit der Fraunhoferschen Anordnung.Literaturverzeichnis
[1] A. J. Fresnel, Ouvre Complétes, Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.[2] H. Boersch, Naturwiss. 28 (1940) 711.
[3] J. Hiller u. E. Ramberg, J. Appl. Phys. 18 (1947)148.
[4] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. London 1704; Opera quae exstant omnis, Ton IV. London 1782; Optik II + III, Übers. W. Abendroth, 0stwald's Klassiker Nr. 97, Engelmann Leipzig 1898; Neuauflage Bd. 96/97 Vieweg, Braunschweig 1983. Optique, Trac. J.P. Murat, 1787; Bourgois, Paris 1989.
[5] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Arbeit 2.
[6] A. Babinet, C. R. 4 (1837) 638.
[7] J. v. Fraunhofer, (Gesammelte Schriften. Verl. bayr. Akad. München 1888.
[8] L. Bergmann u. Cl. Schaefer, Lehrbuch der Experimentalphysik. Bd. III, T 1. Gruyter, Berlin 1956, S. 276.
[9] R. W. Pohl, Einführung in die Optik. Springer, Berlin, Göttingen, Heidelberg 1948, S. 87.
[10] wie [5], Arbeit 1.
[11] M. v. Laue, In: Handb. Experimentalphysik XVIII, Leipzig 1928, S. 307.
[12] A. W. Maue, Z. Naturforschung 4 a (1949) 393.
[13] C. Malgange u. J. Gronkowski, phys. stat. sol. (a) 85 (1984) 389.
[14] M. Born u. W. Biem, Phys. Bl. 25 (1969) 110.
[15] A. W. Lohmann u. S. Sinzinger, J. Opt. Soc. Am. A 9 (1992) 1154.
© 2006 by tediamedia • info@gebeugtes-licht.de