Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie
englisch
Die Newtonschen und Fresnelschen Beugungsexperimente
Photographien der Beugungsfigur des Dreieckspaltes und Grimaldis leuchtender Kante bestätigen Newtons Beobachtungen. Newton beschrieb den Übergang innerer zu äußeren Beugungsstreifen am Dreieckspalt und zeigte, daß gebeugtes Licht nur aus der engen Umgebung jeder Kante (Grimaldis leuchtende Kante) kommt und nicht von der Fläche des Spaltes. Fresnel hingegen teilte nur leicht berechenbare Grenzfälle mit, keine Übergänge innerer zu äußeren Streifen und berücksichtigte nicht die Lokalisierung gebeugten Lichtes. Seit 1850 übernahmen die Lehrbuchautoren Fresnels Theorie und unterschlugen Newtons Beugungsexperimente.
Experimente und Abbildungen
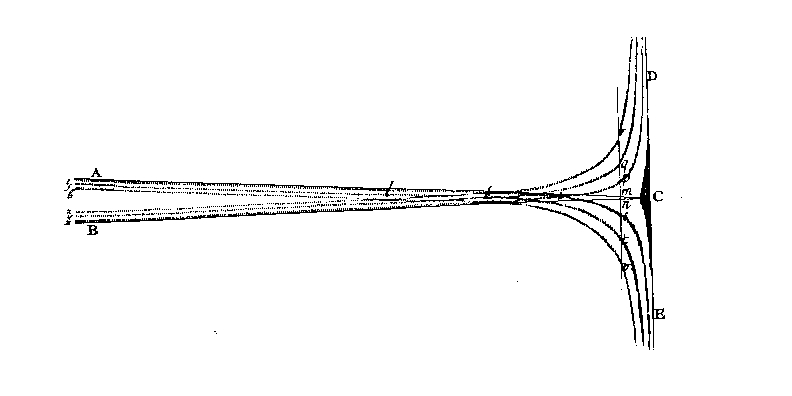
Abb. 1. Die Beugung am Dreieckspalt nach Newton [1] III, Beobachtung 10. Mit Sonnenlicht, einem kleinen Loch im Fensterladen, Entfernung zum Dreieckspalt 10 Fuß und zur Zeichenebene 9 Fuß. ABC Projektion (Schattengrenze) des Dreieckspaltes. Bei Sonnenlicht erhält man drei farbige Beugungsstreifen, mit monochromatischen Licht entprechend mehr.
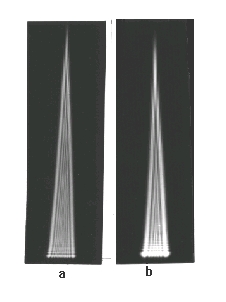
Abb. 2(links). Die Beugungsfigur des Dreieckspaltes bei divergentem Licht. Eine Quecksilber-Höchstdrucklampe mit Grünfilter wurde mit einem Kondensor auf eine Blende vom Durchmesser 0,1 mm abgebildet. In 1 m Entfernung befand sich der Dreieckspalt 0...3 mm.
a: Eine Photoplatte fing die Beugungsfigur in 0,5 m von Spalt auf, zweifach nachvergrößert, Belichtungszeit war den inneren Streifen angepaßt.
b: Photoplatte in 2 m vom Spalt in 0riginalgröße.
Abb. 3(rechts) Die Beugungsfigur eines Dreieckspaltes bei parallelem Licht. Anordnung wie Abb. 2, nur vor dem Dreieckspalt stand eine Linse f' = 1 m, a und b 2fach nachvergrößert.
a: Beugungsfigur in 0,5 m,
b: Beugungsfigur in 2 m Entfernung vom Spalt.
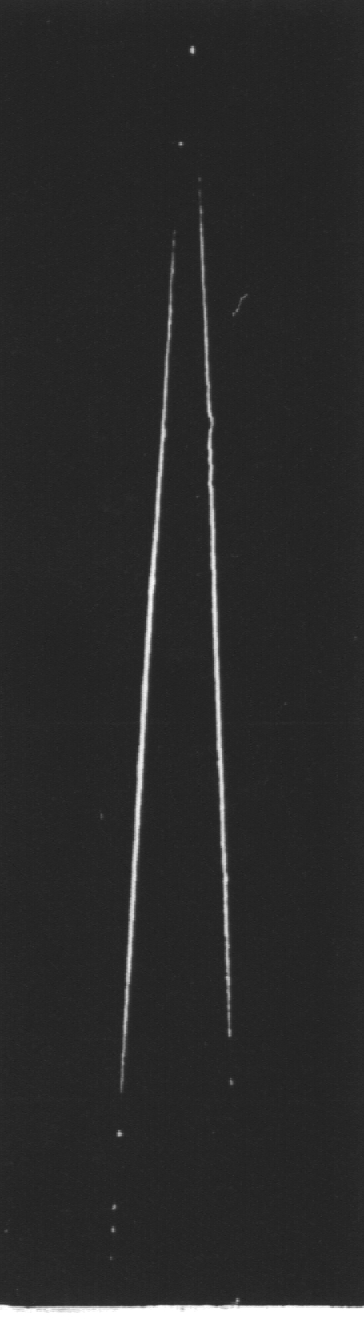Abb. 4. Die leuchtende Kante am Dreieckspalt. Eine Quecksilber-Höchstdrucklampe mit Grünfilter beleuchtete über einen Kondensor eine Durchmesser 0,1 mm Öffnung. In 1 m befand sich der Dreieckspalt, ein Rasierklingenspalt mit 3 mm Basisbreite. Eine Kamera mit doppeltem Bodenauszug und Tessar 1 : 4,5, f' = 13,5 cm war auf den Dreieckspalt scharf eingestellt und so weit seitlich gestellt, daß das direkte Licht neben das Objektiv fiel..
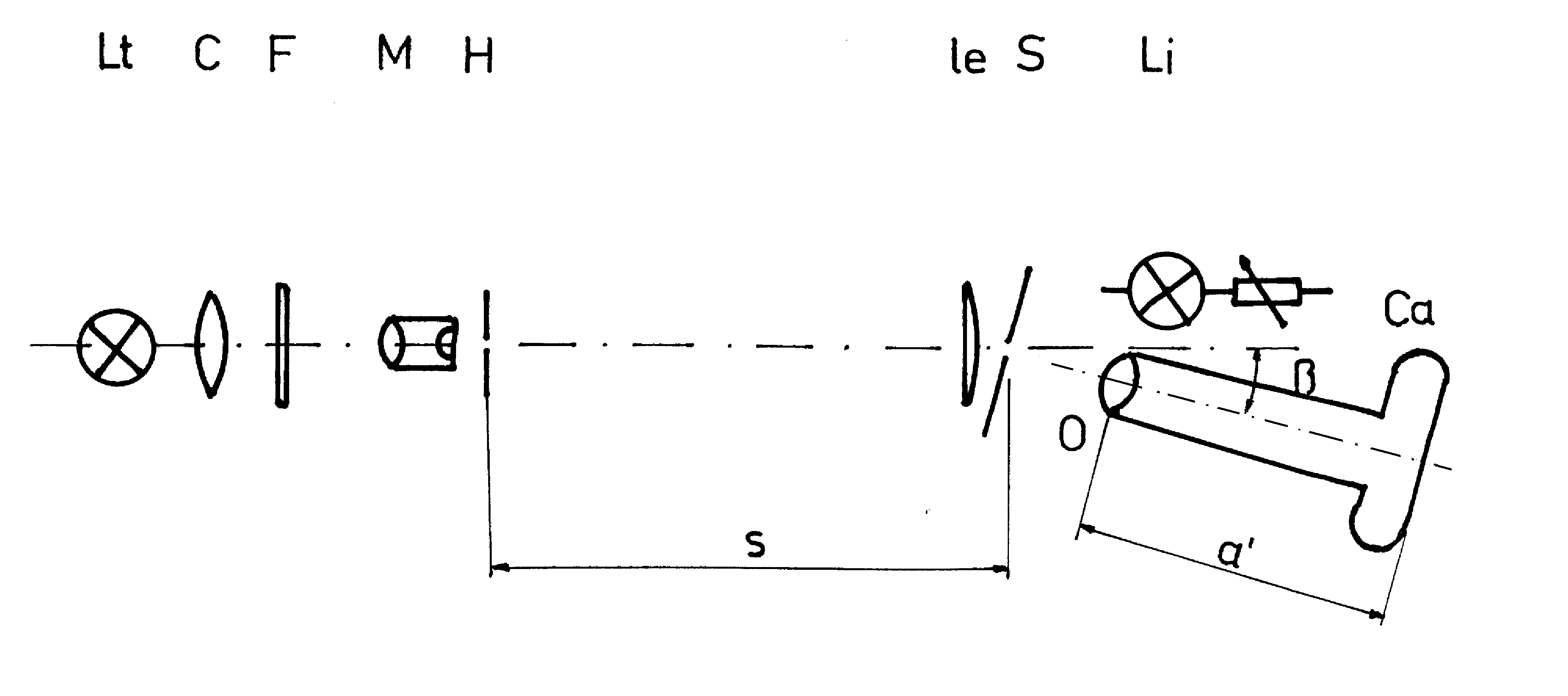
Abb. 5. Experimentelle Anordnung zur Photographie der leuchtenden Kante. Lt - Lichtquelle für Durchlicht, eine Quecksilber-Höchstdrucklampe HBO 100; C - Kondensor; F - Grünfilter; M - Mikroskopobjektiv; H - Kreisblende; Le - Linse für parallele Beleuchtung; S - Spalt 4 mm aus 0,03 mm; Kupferfolie; s - Entfernung von B zu S; Li - Lichtquelle für Auflicht, eine Glühlampe gespeist aus einem Stelltrafo; 0 -Kameraobjektiv Tessar 1 : 2,8, f' = 50 mm; Ca - einäugige Spiegelreflex-Kleinbildkamera mit Zwischenringen; a' - Bildweite = 380 mm. In dieser Abbildung wird die obere Kante als lichtseitige, die untere als schattenseitige bezeichnet.
Lichtseite Schattenseite Lichtseite Schattenseite
Abb. 6. Photographische Aufnahmen eines Spaltes 0,3 mm nach der Anordnung der Abb. 5. Der obere Teil zeigt den Spalt nur im Auflicht, der untere Teil zusätzlich im Durchlicht.a. Ø H = 50 mm, s = 1 m, f' = 50 mm, b = 7°,
b. Ø H = 50 mm, s = 0,5 m, f' = 50 mm, b = 7°,
c. Ø H = 50 mm, s= 1 m, f' = 50 mm, b = 15°,
d.Ø H = 50 mm, s = 1 m, f' = 50 mm, b = 30°.
Abb. 7. Wie Abb. 6, aber:
a. Ø H = 50 mm, s = 1 m, f' = 135 mm, b = 7°,
b. Ø H = 50 mm, s = 1 m, f' = 135 mm, b = 14°,
c. Ø H = 50 mm, s = 1 m, f'= 10 mm, b = 7°,
d. Ø H= 50 mm, s = 1 m, f' = 10 mm, b = 14°.
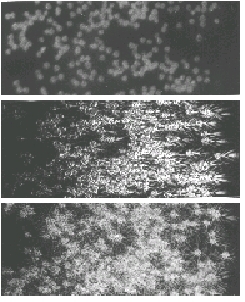
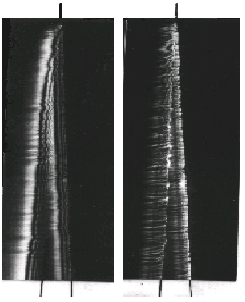
Abb. 8. Photographische Aufnahmen der Streufiguren von Bärlappsporen in der Apparatur der Abb. 5, aber statt Li 1 bis F ein He-Ne Laser 188 und statt S eine Glasplatte mit Bärlappsporen, Abbildungsmaßstab wie Abb. 6.
a. Nur Auflicht,
b. Nur Durchlicht, b = 7°,
c. Nur Durchlicht, b = 15°
Abb. 9. Photographische Aufnahme der Spitze des Dreieckspaltes in der Apparatur der Abb. 5, im gleichen Abbildungsmaßstab wie Abb. 6. ,Ø B = 0,5 mm, s = 1 m, Die Striche deuten die Lage der Projektion des Spaltes an.
a. b = 7°
b. b=15°
Folgerungen
Fresnel bestätigte in seiner ersten Arbeit über die Beugung, daß gebeugtes Licht nur 'von den Kanten' kommt, konnte damit aber die inneren Beugungsstreifen des Hindernisses (und äußere des Spaltes) nicht berechnen. Auch hatte er festgestellt, daß am Spalt das Gebiet zwischen den gebeugten Bereichen nicht einfach abgedeckt werden darf. Tut man dies, so erhält man die Beugungsfigur des Doppelspaltes. Daher nahm er in der zweiten Arbeit das Huygensschen Prinzip als vorgegeben an. Den physikalischen Widerspruch der Herkunft des gebeugten Lichtes berücksichtigte er nicht mehr, ihn genügte die mathematische Darstellung in großen Entfernungen und er zeichnete seine Wellen als Kreise später nicht bis zum Hindernis. Fresnel war sich also der Schwächen seiner Theorie bewußt. Die Lehrbuchautoren ab 1850 ließen Newtons Beugungsexperimente weg und konnten so eine einfache aber irreführende Beschreibung der Beugung vortäuschen. Daß das Gebiet zwischen den Bereichen, aus denen gebeugtes Licht kommt, nicht abgedeckt werden darf, muß in späteren Arbeiten begründet werden, es rechtfertigt aber nicht die Extrapolation. Man kann zusammenfassen, daß Fresnel in späteren Arbeiten
- Die Beugung an der Halbebene, mit ungleichmäßigen Abständen der Beugungsstreifen, mittels Fouriertheorem mit dem Fresnelintegral, Huygensschen Prinzip und Youngs Interferenzprinzip, berechnen konnte.
- Die Beugung am Hindernis mit inneren und am Spalt mit äußeren Beugungsstreifen, mit konstanten Abständen der Beugungsstreifen, mit dem Fouriertheorem mit Winkelfunktionen der Formel (1) berechnen konnte. Insbesondere Punkt 2 ist aber nur in sehr großen Entfernungen gültig
- Gebeugtes Licht kommt nach Newton nur aus der engen Umgebung der Kante, nach Young und Fresnel fälschlich nur von der Kante.
- Die Beugung am Dreieckspalt demonstriert, daß in kurzen Entfernungen und großen Spaltweiten die inneren Beugungsstreifen des Spaltes (bzw. die äußeren des Hindernisses) entstehen, die der Beugungsfigur der Halbebene mit den Kante als Halbebenen entsprechen. Erst in größeren Entfernungen entstehen die äußeren Beugungsstreifen des Spaltes (bzw. die inneren des Hindernisses), die in Lehrbüchern nach 1850 als einzige Beugungsfigur des Spaltes angegeben wurden. Erst hier kommt also die unzulässige und falsche Extrapolation zur Geltung.
© 2006 by tediamedia • info@gebeugtes-licht.de