
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Die Weiterführung der Newtonschen Beugungsexperimente
In einer Schlierenapparatur werden Newtonsche Beugungsexperimente weitergeführt. Das Spaltbild besteht aus einem Doppelstreifen mit dunklem Zwischenstreifen am Ort des Bildes dieser Kante. Dies war nach den Newtonschen Beugungsexperimenten zu erwarten, aber mit wesentlichen Ergänzungen. Die Breite des Doppelstreifens beträgt < 0,1 mm, abhängig von der Apertur der Abbildung. Durch Abdecken von Ordnungen in der Beugungsfigur können je Ordnung zwei Orte im Bild des Spaltes gefunden werden. Eine Zuordnung innerhalb der Ordnung gelang nicht. Technische Anwendungen in der Meßtechnik, diffractiver Optik und beugungsbegrenzter Optik werden aufgezeigt.
Experimente und Abbildungen
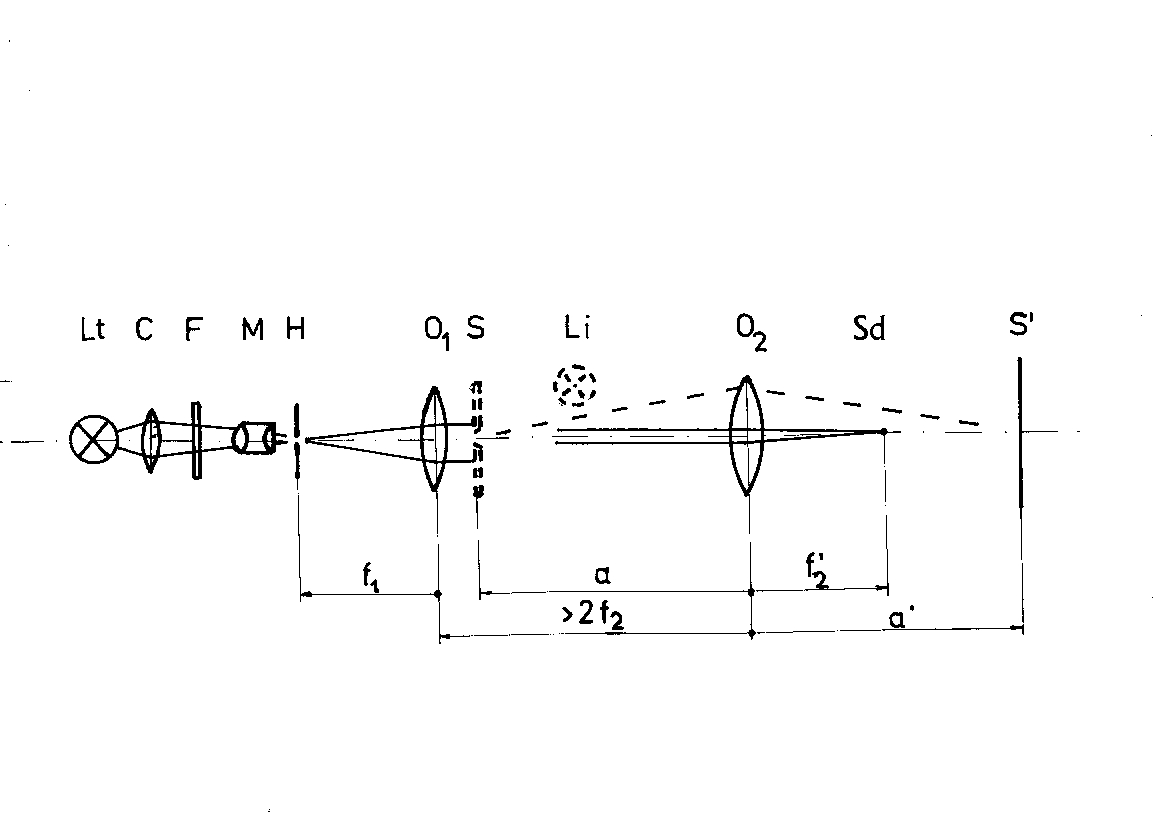
Abb. 1. Schlierenapparatur nach Abbe. Lt - Lichtquelle, z. B. Quecksilber-Höchstdrucklampe; c - Kondensor; F - z. B. Grünfilter; Lt, C und F können durch einen Laser ersetzt werden; M - Mikroskopobjektiv; H - Lochblende; O1 - Objektiv; S - Beugungsspalt; Li - Beleuchtung für Auflicht; O2 - Abbildungsobjektiv, Brennweite 200 ... 400 mm; SD - Schlierenblende, etwa eine kleine Kugel, z. B. aus Knete, oder auch ein Keil, etwas größer als H'; S' - Bild des Spaltes S. Dieses Bild kann mit einer Lupe betrachtet werden, hier kann ein Schirm oder die Photoschicht einer Fernseh-Aufnahmekamera stehen. Gestrichelte Linien deuten gebeugtes Licht an.
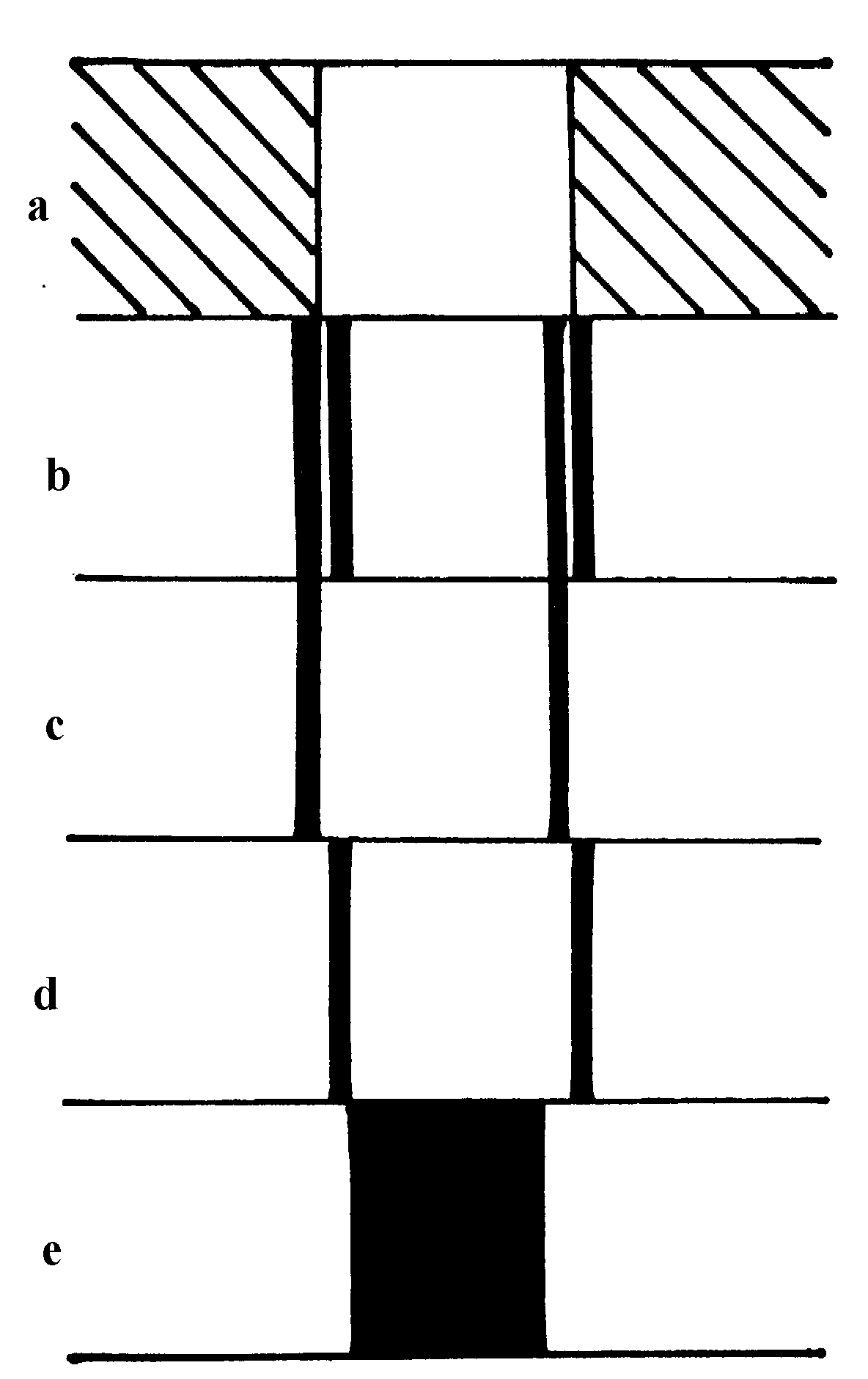
Abb. 2. Strichzeichnung der Ergebnisse des Schauversuchs mit der Apparatur nach Abb. 1. a. Bild des Spaltes im Auflicht. b. Bild des Spaltes in der Schlie renapparatur. c. Spaltbild wenn eine Seite der Beugungsfigur vor dem Ab bildungobjektiv abgedeckt wurde. d. Die andere Seite abgedeckt. e. Schlierenblende durch eine Lochblende ersetzt, nur die nullte Ordnung erzeugte das Spaltbild.
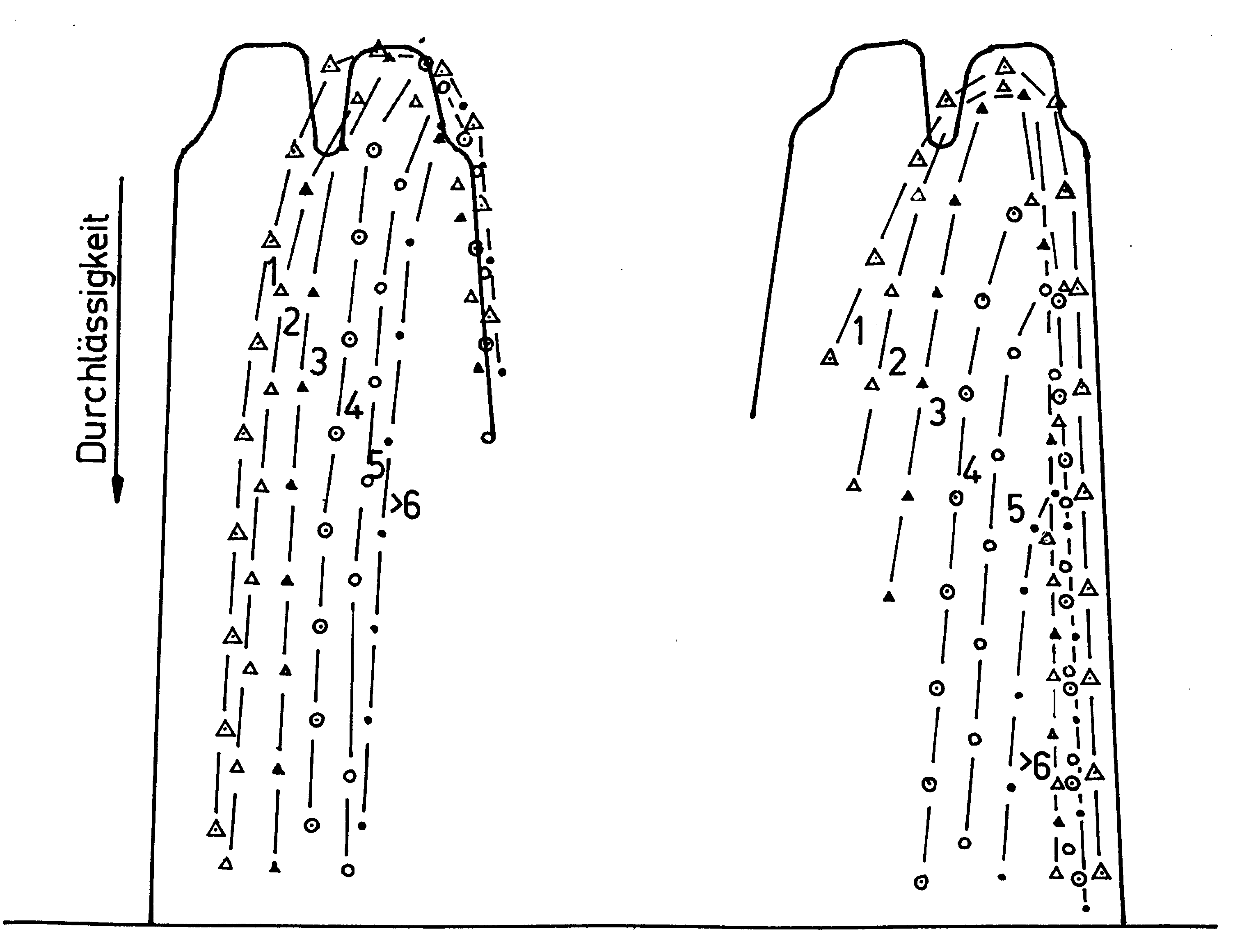
Abb. 3. Photometerkurven der Negative des Spaltbildes in der Schlierenapparatur Abb. 1 mit schrittweise abgedeckter Beugungsfigur vor O2. H - 0,5 mm Ø, S - 0,2 mm, a'/a = - 5. Alle Negative waren mit der gleichen Belichtungszeit auf der gleichen Platte untereinander aufgenommen und mit der gleichen Einstellung photometriert. Ausgezogene Kurven - unabgedeckt. ● - eine Seite und darüber hinaus bis einschließlich der 5. Ordnung abgedeckt, ο- bis zur 4. Ordnung, ⊗ - bis zur 3. Ordnung, ▲ - bis zur 2. Ordnung, Δ - bis zur 1. Ordnung, ∇ - bis zur 0. Ordnung abgedeckt&;.
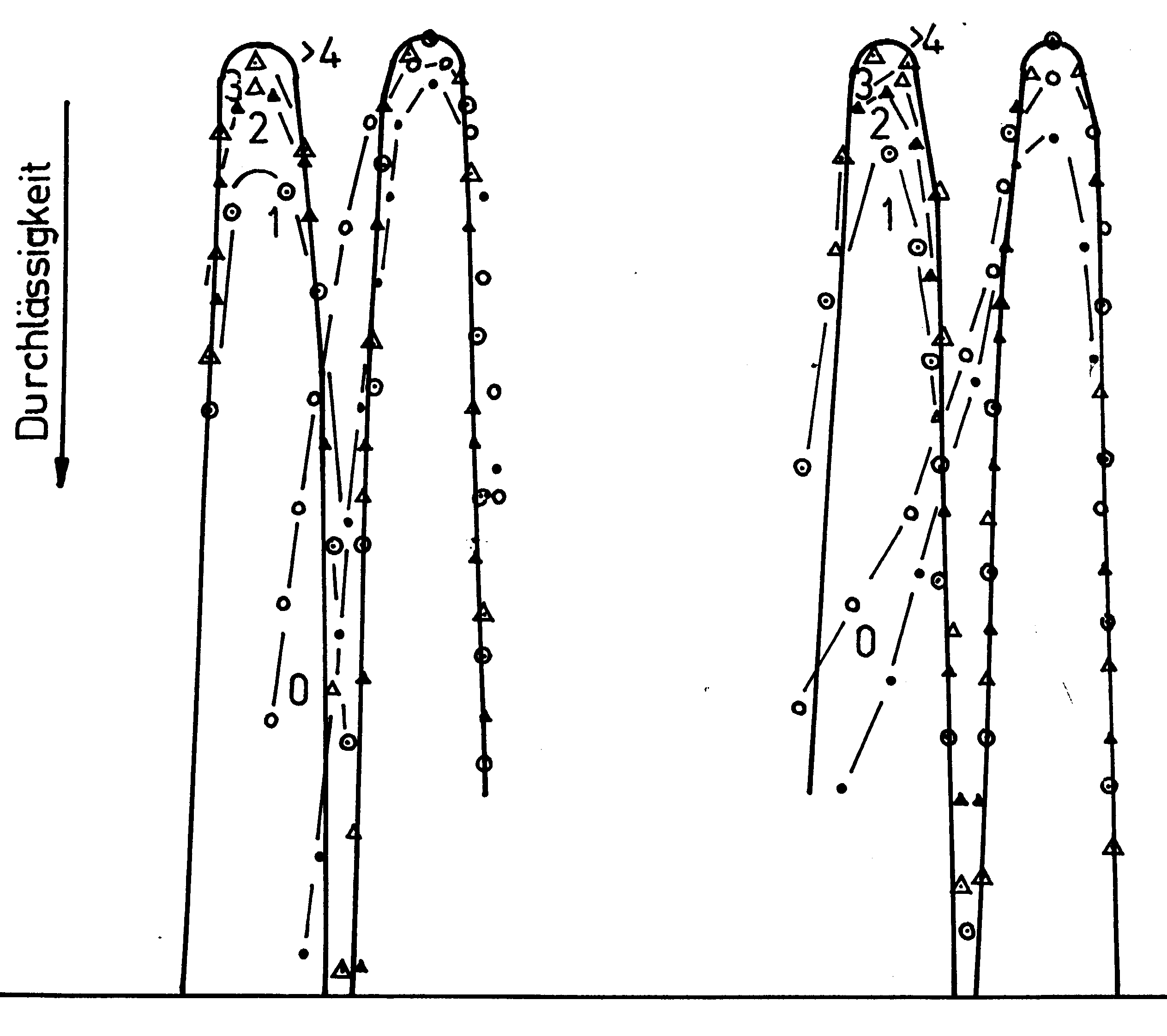
Abb. 4. Wie Abb. 3 mit kürzerer Belichtungszeit und neuer Einstellung. Eine Seite der Beugungsordnungen war stets frei, ● - eine Seite und die 0. Ordnung abgedeckt, ο- eine Seite und die nullte Ordnung frei, ⊗- noch die 1. Ordnung frei, ▲ - noch die 2. Ordnung frei, Δ - noch die 3. Ordnung frei ∇ - noch die 4. Ordnung frei.

Abb. 5 Bild des Spaltes 0,25 mm in einer Schlierenapparatur nach Abb. 1 im Abbildungsmaßstab a' / a = 1 / -1. 30o schräg vor der Abbildungsoptik die Beugungsfigur abgedeckt mit 12 sichtbaren Ordnungen. O1 und O2 - f' = 320 mm, 10 fach nachvergrößert. a. Film stand knapp vor der Überkreuzungsstelle der schatten- und lichtseitigen Streifen. b. Film knapp hinter dieser Ebene.
Allgemeine Diskussion
Man wird hiernach die Frage stellen, wieso bei diesem Sachverhalt sich die von Fresnelsche durchgesetzte Wellenauffassung des Lichtes so lange halten konnte. Die Antwort ist einfach: Newton und seine Nachfolger konnten mit Lichtteilchen, die nur als Massepunkte vorstellbar waren, die Beugung nicht begründen, denn dazu war eine Kraft senkrecht zur Ausbreitungsrichtung des Lichtes notwendig, die die Newtonsche Mechanik nicht vorsieht. Die Wellentheorie dagegen konnte für große Entfernungen eine Berechnung und eine Erklärung bieten, die für wichtiger gehalten wurde als deren experimentelle Sicherung. So wurden die die Wellentheorie widerlegenden Newtonschen Beugungsexperimente von den Lehrbuchautoren ab etwa 1850 einfach weggelassen. Als Anfang unseres Jahrhunderts die Quantennatur des Lichtes entdeckt wurde, hätte man eigentlich Newton recht geben müssen, aber am Sachverhalt, daß auch weiterhin mit massepunktförmigen Lichtquanten oder Photonen die Beugung nicht zu erklären war, hatte sich nichts geändert. So blieb man für die Beugung bei der Fresnelschen Wellenanschauung.
Newton hatte also recht, wenn er behauptete, daß Licht niemals eine Welle sein kann, mit der Lokalisierung des gebeugten Lichtes hatte er das bewiesen. Marshall [16] diskutierte über die Lokalitäts-Debatte, die Newtonschen Beugungsexperimente bringen aber die entscheidenden Argumente für den lokalen Realismus. Es gibt also keinen Zweifel: Die Extrapolation der Gültigkeit der äußeren Beugungsstreifen am Spalt (Formel (1) bei Nieke [1]) auf die Entfernung Null oder in die Spaltebene war unzulässig und falsch.
Die Bemerkung, daß für Lichtteilchen, Lichtquanten oder Photonen als Massepunkte eine Erklärung nicht möglich war, läßt vermuten, daß für Teilchen mit Raumerfüllung, also für Photonen mit Struktur eine Erklärung der Beugung möglich sein könnte. In der Tat ordnet man ab etwa 1960 allen Elementarteilchen eine Struktur zu, dazu ist etwa der Name Hofstadter [17] zu nennen. Auch schwere Elementarteilchen und Atome zeigen die Erscheinung der Beugung, wie z. B. Carnal u. Mlynek [18] berichteten. Diese Korpuskeln haben unbestritten eine Struktur und so könnten auch Photonen und Elektronen eine Struktur haben, die Beugung als Ablenkung bedingt,. denn bei Atomen wird niemand annehmen, daß sie sich auslöschen. Aber dazu sollen erst noch weitere Experimente in späteren Arbeiten vorgelegt werden, um dann zu ausreichenden Kenntnissen zu kommen, die eine Deutung zulassen.
Literaturverzeichnis
[1] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Arbeit 1.[2] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and (Colours of Light.. London 1704); Opera quae exstant omnis, Tom IV, London 1782; Reprint Bruxells 1966; Optitk II + III, Übers W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmann, Leipzig 1998; Neuauflage: Bd 96/97, Vieweg, Braunsonweig 1983 0ptique, Trac. J. P. Marat 1787; Bourgois, Paris 1989.
[3] A. J. Fresnel, Oeuvre Completes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926
[4] S. Banerji, Philos. Mag.(6) 37 (1919) 112.
[5] K. Noack, Phys. Z. 23 (1922) 228.
[6] M. v. Laue, in: Handbuch der Experimentalphysik Bd. 18 Akad. Verlagsges., Leipzig 1928, S. 349-350.
[7] H. K. V. Lotsch, Die Strahlenversetzung bei Totalreflexion: Der Goos-Hänchen-Effekt. Diss. T. H. Aachen 1970.
[8] K. H. Brauer u. F. Fröhlich, Experim. Techn. d. Physik 6 (1958) 216, Abb. 4.
[9] W. Heisenberg, Die physikalischen Prinzipien der Quantentheorie. 2. Aufl., Hirzel, Leipzig. 1941. S. 9 - 14, 57 - 59. The physical principles of quantum theory, Univ, Press, Chicago 1930.
[10] H. Arndt u. H. Nieke, Z. Psychologie 193 (1985) 295.
[11] H. Nieke, Exper. Techn. Physik 31 (1983) 119.
[12] S. Ganci, Am. J. Phys. 57 (1989) 370.
[13] A. Rubinowicz, Ann. Physik (4) 53 (1917) 258; 73 (192.7) 339.
[14] Ch. Hofmann, Fortschr. Physik 27 (1979) 595; Exper. Techn. Physik 28 (1980) 403.
[15] K. Knop, Phys. Bl. 47 (1991) 901, Zitat S. 904
[16] T. W. Marshall, Found. Phys. 22 (1992) 363.
[17] R. Hofstadter, Rev. Mod. Phys. 28 (1956) 214 Phys. Bl. 18 (1962) 193.
[18] O.Carnal u. J. Mlynek, Phys. Bl. 47 (1991) 379; Phys. Rev. Lett. 66 (1991) Nr. 21, 2639-96
© 2006 by tediamedia • info@gebeugtes-licht.de