
Die Newtonschen und Fresnelschen Beugungsexperimente
Die Weiterführung der Newtonschen Beugungsexperimente
Beugung von Licht an Spalt und Hindernis
Interferenz-Winkelbedingung, Beugung und
Abbildung
Beugungen hintereinander folgend und mit
Zwischenabbildung
Frequenzminderung nach der Beugung
Innere und äußere Beugungsstreifen von
Kreisöffnungen
Überlagerung von Interferenz und Beugung
Beugungsexperimente mit inhomogener
Beleuchtung
Experimente mit polarisiertem Licht mit
Spalt und Doppelspalt
Der Untergrund von Beugungsfiguren
Versuch der Deutung der Newtonschen
Beugungsexperimente
Folgerungen aus den Newtonschen
Beugungsexperimenten für Photonen
Folgerungen für die Struktur des
Elektrons aus der des Photons
Das thermisch bedingte elektromagnetische
Feld
Beugung und Lichtemission von
Elektronen
Energiestufen der Elektronen im
magnetischen Eigenfeld
Faradays elektro-tonische Zustände
Nahfeldoptik mit Berücksichtigung der
Newtonschen Beugungsexperimente
Die Berücksichtigung der magnetischen
Momente in der Quantentheorie

Interferenz-Winkelbedingung, Beugung und Abbildung
Die sog. Kohärenzbedingung beinhaltet eine geometrischen Beziehung, wo der Winkel zur (konventionellen) Lichtquelle kleiner sein muß als der zum Abstand der Beugungsstreifen. Das Wirken einer Ordnung der Strahlung besteht hier nicht, daher wird die Bezeichnung Interferenz-Winkelbedingung vorgeschlagen. In Fraunhoferscher Beobachtungsart treten außerhalb der Brennebene auch innere Beugungsstreifen des Spaltes auf. In der Entfernung der doppelten Brennweite entstehen bei paralleler Einstrahlung mit und ohne Optik die gleichen Beugungsfiguren des Spaltes mit inneren und äußeren Beugungsstreifen, nur mit Optik auf dem Kopf stehend. Interferenz-Winkelbedingung und Abbesche Theorie ergänzen sich bei der Abbildung im Mikroskop.
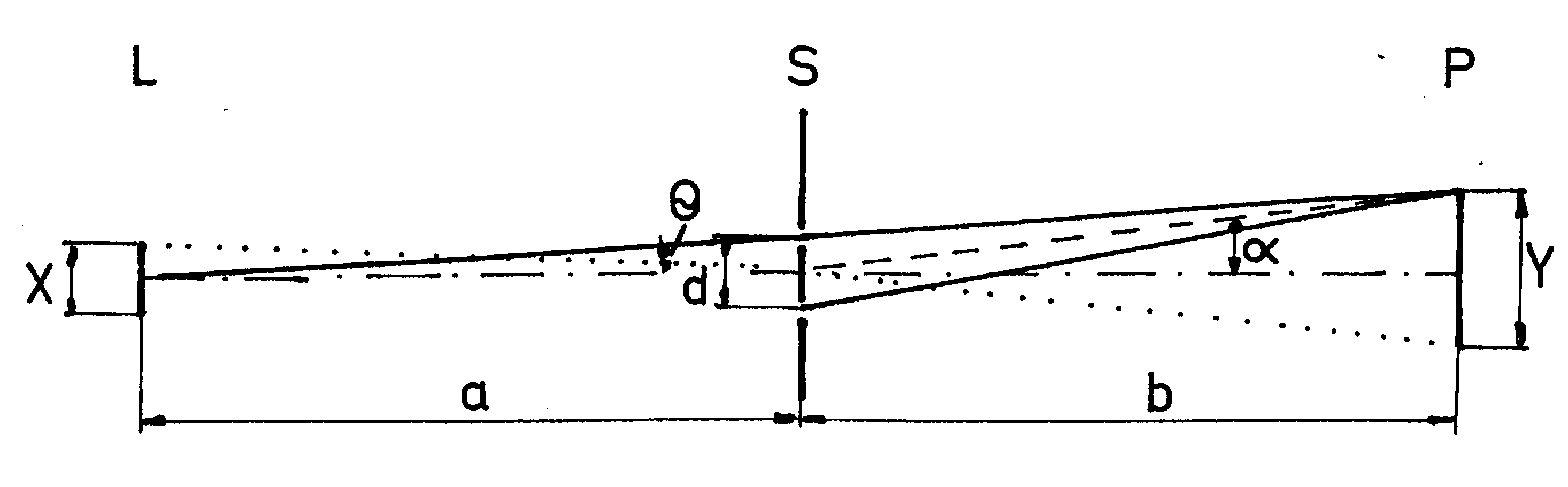
Abb. 1. Schematische Darstellung von Lichtquelle und Doppel-spalt zur Ableitung der sog. Kohärenzbedingung. L - Lichtquelle der Ausdehnung X; S. Doppelspalt mit dem Spaltabstand d; P - Auffangfläche mit dem ersten Beugungsminimum vom Abstand Y; Θ - halber Öffnungswinkel; α - Beugungswinkel.
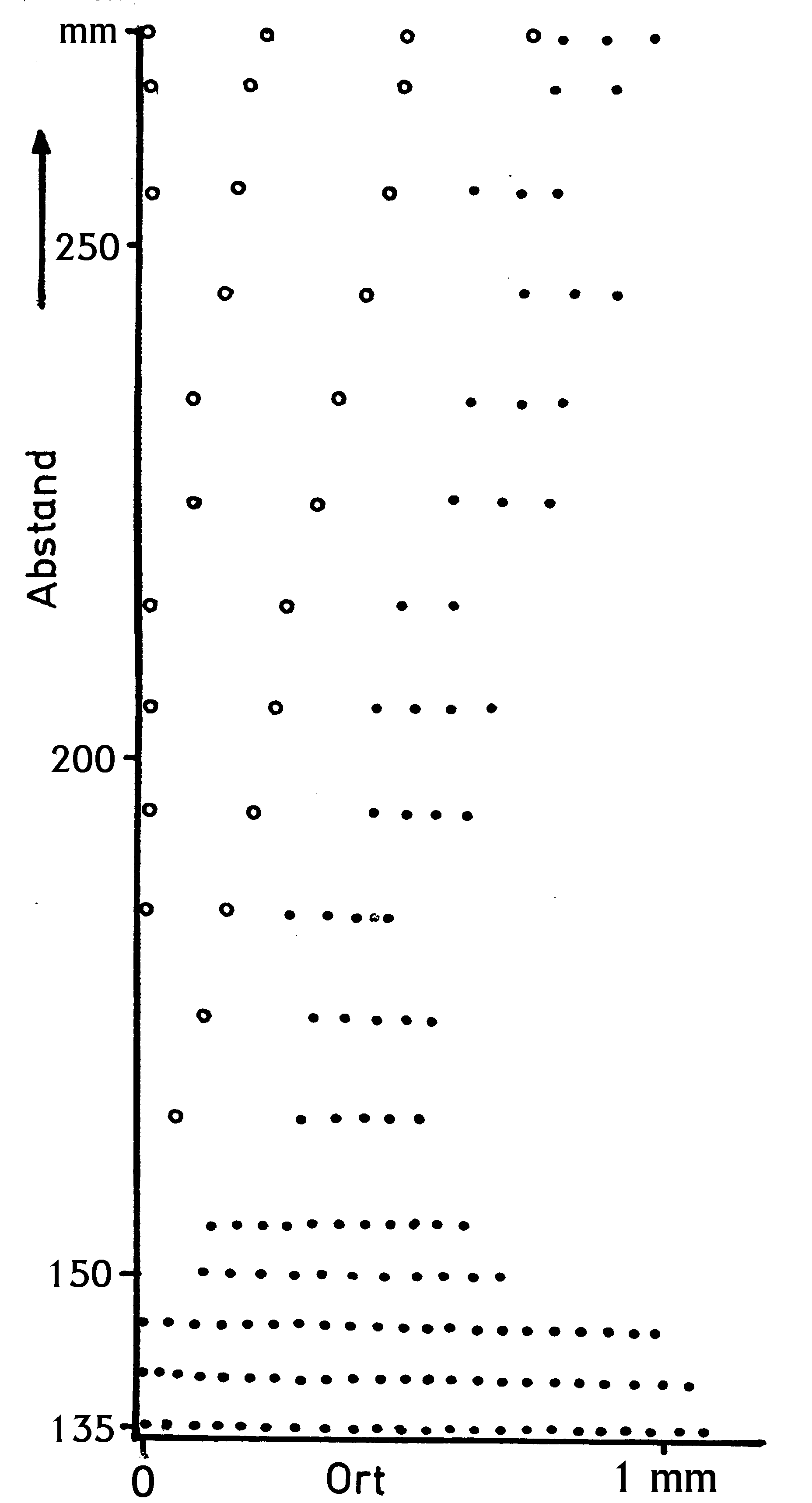
Abb. 2. Die Lage der Maxima innerer und äußerer Beugungsstreifen am Spalt zwischen einfacher und doppelter Brennweite, in Fraunhoferscher Beobachtungsart, f' = 135mm. ο- Maxima innerer Streifen, • - Maxima äußerer Streifen. Das äußerste Auftreten innerer Beugungsstreifen markiert die Schattengrenze.
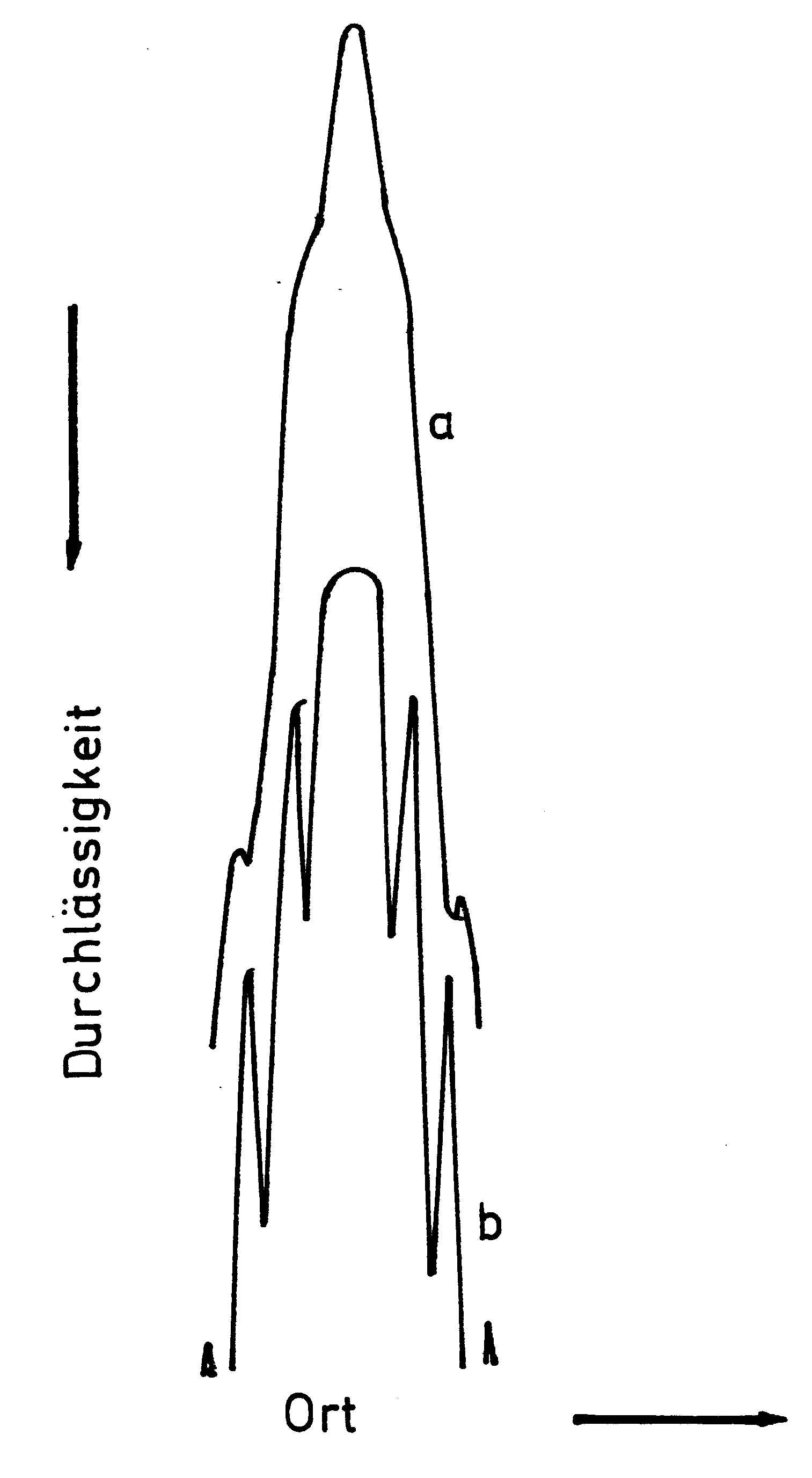
Abb. 3. Photometerkurven von Beugungsfiguren mit 0,6 mm Spaltweite. Beleuchtungsspalt 0,001 mm, Tessar f' = 135 mm als Kollimator, a: ohne weitere Optik in 140 mm Entfernung, b: Objektiv f' = 140 mm.
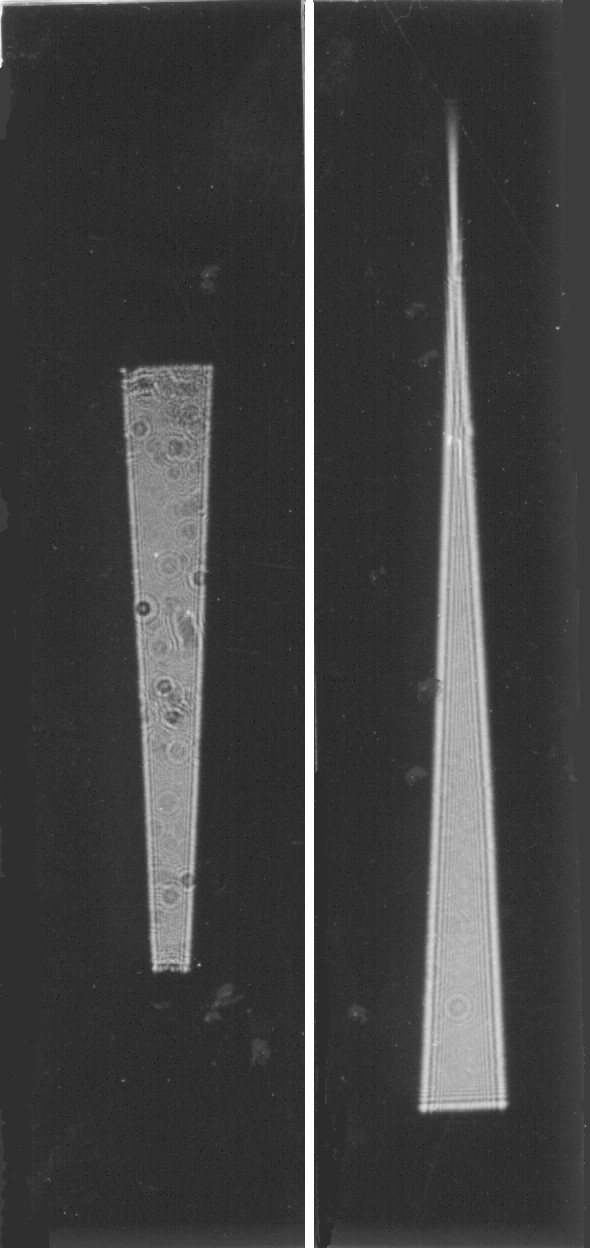
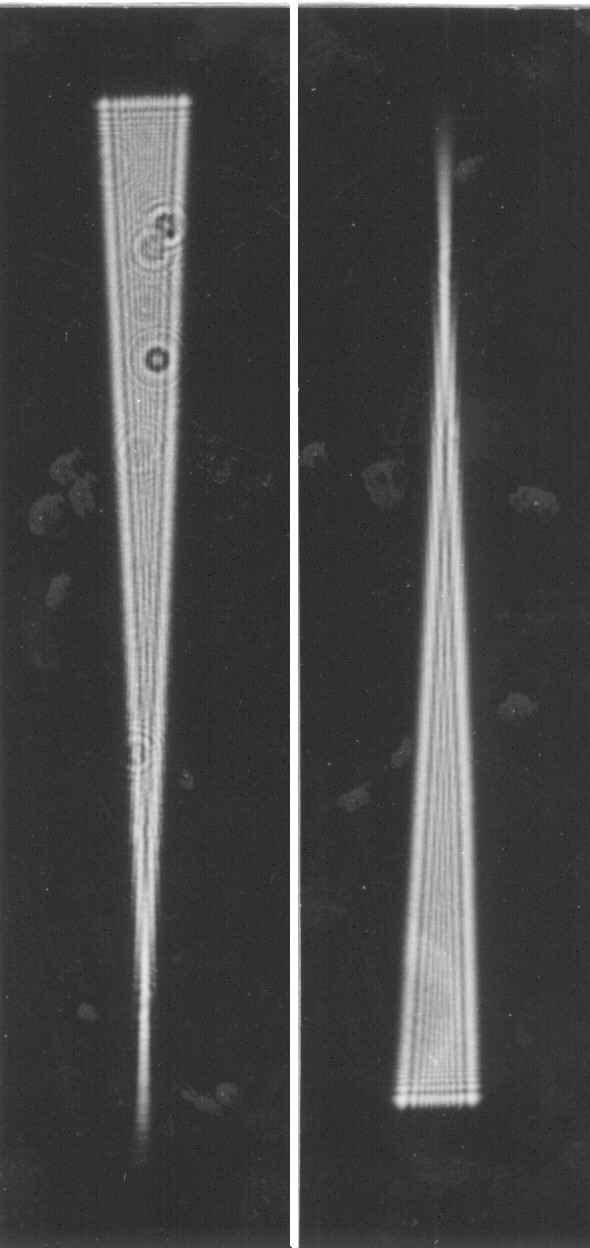
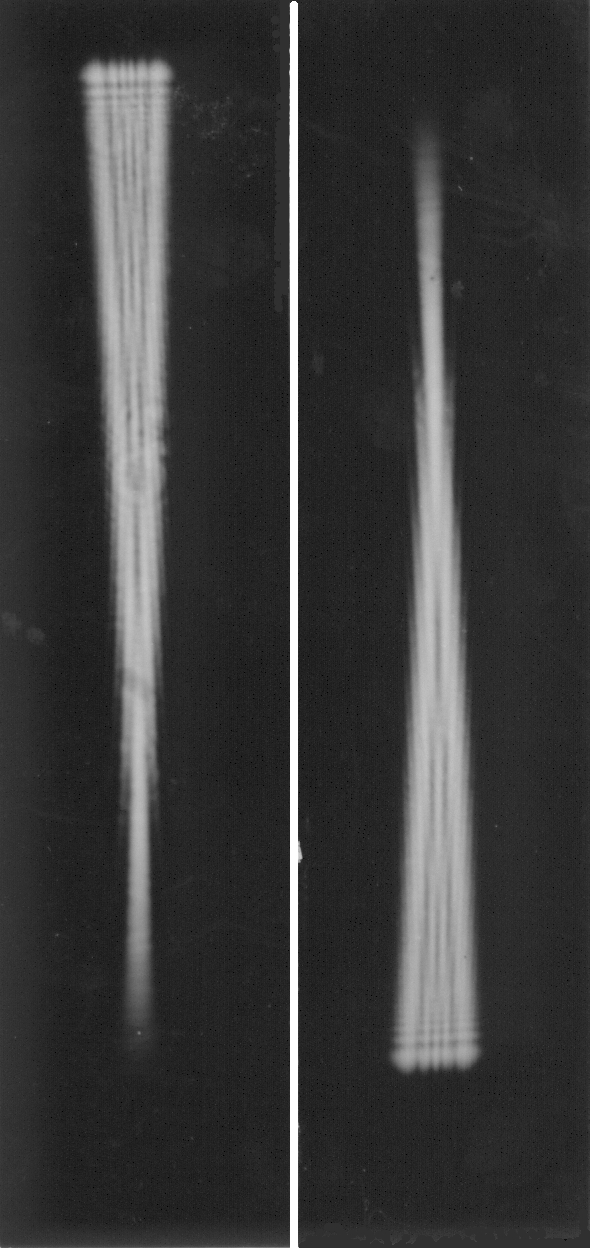
Abb. 4 (links). Beugungsfigur in der doppelten Brennweite. Eine Hg-Höchstdrucklampe HBO 100 mit Grünfilter und Kondensor beleuchte eine Lochblende 0,1 mm, in 1 m Entfernung stand eine Linse f'= 1 m, dahinter ein Dreieckspalt 0.. .3 mm, der so parallel beleuchtet wurde. Dahinter : a: Ein Tessar 1 : 2,8, f' = 50 mm, Beugungsfigur in 100 mm Entfernung, b: Objektiv entfernt, Beugungsfigur in 100 mm Entfernung.
Abb. 5 (mitte) Wie Abb. 4. a: Mit Tessar 1 : 4,5, f' = 135 mm in 270 mm Entfernung, b: Objektiv entfernt, Beugungsfigur in 270 mm Entfernung.
Abb. 6 (rechts). Wie Abb. 4. a: Achromat 1 : 8, f' = 320mm in 640 mm Entfernung, b: Objektiv entfernt, Beugungsfigur in 640 mm Entfernung,
Diskussion
Die Analogie zu Wasserwellen legte früher nahe, auch für Licht als Welle Ordnungszustände oder Phasenbeziehungen anzunehmen. Aber bereits Maxwell [30] betrachtete Licht als elektromagnetische Störung, er rechnete allerdings auch mit Wellen.
Mit Hilfe der Interferenz-Winkelbedingung konnte gezeigt werden, daß die Wellenanschauung der sog. Kohärenzbedingung dort eigentlich nie notwendig war, denn sie ist rein geometrisch interpretierbar.
Beim Thema Beugung und Abbildung ist zu berücksichtigen, daß innere und äußere Beugungsstreifen am Spalt unterschiedliche Entfernungsabhängigkeiten aufweisen. Allgemein ist bekannt, daß die Abstände äußerer Beugungsstreifen am Spalt linear mit der Entfernung wachsen, die Photonen laufen also geradlinig. Anders die Abstände innere Beugungsstreifen des Spaltes oder die Beugungsstreifen der Halbebene. Hier fand Fresnel [19] experimentell ein anderes Verhalten. Es genügt dazu die parallele Lichteinstrahlung zu beachten, wo die Abstände der Beugungsstreifen nur mit der Wurzel aus der Entfernung wachsen (genaueres bei Nieke [24]). Newton [20] III Frage 3 schloß aus dem Übergang der inneren zu äußeren Beugungsstreifen am Dreieckspalt, daß sich die Lichtteilchen aalartig bewegen müßten. Nach Nieke [22], [23] und [24] ist das schattenseitig gebeugte Licht schattenseitig versetzt, also auch hier können die Photonen nicht geradlinig laufen, sondern in einer S-Kurve, denn von den Spaltbacken können sie nicht kommen. So ist sicher, daß Beugung und Abbildung nicht einheitlich zu beschreiben sind, sondern für innere und äußere Streifen unterschiedlich.
Literaturverzeichnis
[1] M. E. Verdet, Ann. Sci. L'École Norm. Super. (Paris) 2 (1865) 291.
[2] E. Berge, Math. naturwiss. Unterricht 27 (1974) 326.
[3] W. Arkadiew, Phys. Z 14 (1913) 832.
[4] P. H. Cittert, Physica 1 (1934) 201.
[5] F. Zernicke, Physica 5 (1938) 785.
[6] S. I. Wawilow, Die Mikrostruktur des Lichtes. Akademie-Verlag, Berlin 1954, S. 62, 76 u. 84.
[7] G. T. Reynolds, K. Spartalian u. D. E. Scarl, Nuovo chim. 61 B (1969) 355.
[8] P. A. M. Dirac, Die Prinzipien der Quantenmechanik. Hirzel, Leipzig 1930. The Principles of Quantum Mechanics. Clarendon Press Oxford 1935, 1947, 1958.
[9] P. L. Kapitza u. P. A. M. Dirac, Proc. Cambridge Phil. Soc. 28 (1933) 297.
[10] H. Schwarz, Z. Phys. 204 (1967) 276; Phys. Bl. 26 (1970) 436.
[11] G. Magyar u. L. Mandel, Nature 198 (1963) 255.
[12] G. Richter, W. Brunner u. H. Paul, Ann. Physik (7) 14 (1964) 239.
[13] R. J. Glauber, Phys. Rev. 130 (1963) 2529; 131 (1963) 2766
. [14] J. F. Vinson, Optische Kohärenz. WIB 85, Akademie-Verlag Berlin, Pergamon Press, Oxford, Vie weg Braunschweig 1971.
[15] H. Nieke, Exp. Techn. Physik 31 (1983) 53.
[16] E. Schrödinger, Ann. Physik (IV) 61 (1920) 69.
[17] A. Einstein, Phys. Z. 18 (1917) 121.
[18] E. Schrödinger, Nature and the Greeks. Univ. Press Cambridge 1954; Die Natur und die Griechen. Rowohlt Nr. 28, Hamburg 1956, S. 35.
[19] A. J. Fresnel, Oeuvre Complétes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.
[20] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. Lon don 1704. Opera quae extant omnis, Tom IV, London 1782; Optik II +III. Übers. W. Abendroth, 0stwald's Klassiker Nr. 97. Engelmann, Leipzig 1898; Neuauflage Bd 96/97, Vieweg, Braunschweig 1983; Optique, Trac..J. P. Marat 1787; Bourgois, Paris 1989
[21] J. v. Fraunhofer, Gesammelte Schriften. Verl. bayr. Akad. München 1988.
[22] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Arbeit 1.
[23] Wie [22] Arbeit 2.
[24] Wie [22], Arbeit 3.
[25] F. Zernicke, Physica 9 (1942) 686.
[26] F. T. S. Yu, in Ed. F. Wolf: Progress in Optics XXIII (1986) 222.
[27] K. Pietsch u. E. Menzel, Optik 12 (1955) 203.
[28] W. Messerschmidt, Optik 12 (1955) 297.
[29] E. Menzel u. W. Miradé u.,I. Weinberger, Fourieroptik und Holographie. Springer, Wien u. New York 1973, Zitat im Vorwort.
[30] J. C. Maxwell, The scientific papers. Cambridge 1890; Hrsg. L. Boltzmann, Über physikalische Kraftlinien. Ostwalds Klassiker Nr. 102, Engelmann, Leipzig 1898.
[31] E. Panarella, Speculations Sci.Techn. 8 (1985) 35.
[32] S. Jeffers, R. Wadlinger a. G, Hunter, Can. J. Phys. 69 (1991) 1471.
© 2006 by tediamedia • info@gebeugtes-licht.de