
Newton's and Fresnel's Diffraction Experiments
The Continuation of Newton's Diffraction
Experiments
Diffraction of Light at Slit and Hindrance
Interference-Angle Condition, Diffraction and
Imagery
Diffraction One After Another and with
Intermediate Imagery
Diminishing of Frequency of Light after
Diffraction
Inner and Outer Diffraction-Fringes at
Circular Openings
Superposition of Interference and Diffraction
Diffraction Experiments with Inhomogeneous
Illumination
Experiments with Polarized Light at Slit and
Double-Slit
The Background of Diffraction-Figures
Trial for Interpretation of Newton's Diffraction
Experiments
Consequences for Photons out of Newton's
Diffraction Experiments
Consequences for Structure of Electrons out of
that of Photons
The Thermally Conditioned Electromagnetic Field
Diffraction and Light-Emission of Electrons
Energy-Steps of Electrons in Magnetic Eigen-Field
Faraday's Electro-tonic States
Near-Field Optics with Regard to Newton's
Diffraction-Experiments
Consideration of Magnetic Moment of Electron
in Quantum Theories

The Continuation of Newton's Diffraction Experiments
Newton's diffraction experiments are continued in a schlieren apparatus. The image of slit consists of a double-stripe with a small dark space at ever place of the image of an edge. This is to expect by Newton's diffraction experiments but with new details. The breadth of a double-stripe is < 0.l mm dependent to aperture of imagery. With masking of orders in the diffraction figure can determine ever order two places of bent light in the slit image. An attaching within the order did not succeed. Measurement technique, diffractive-optics and diffraction-limited-optics are fields of technical applications.
Experiments and results
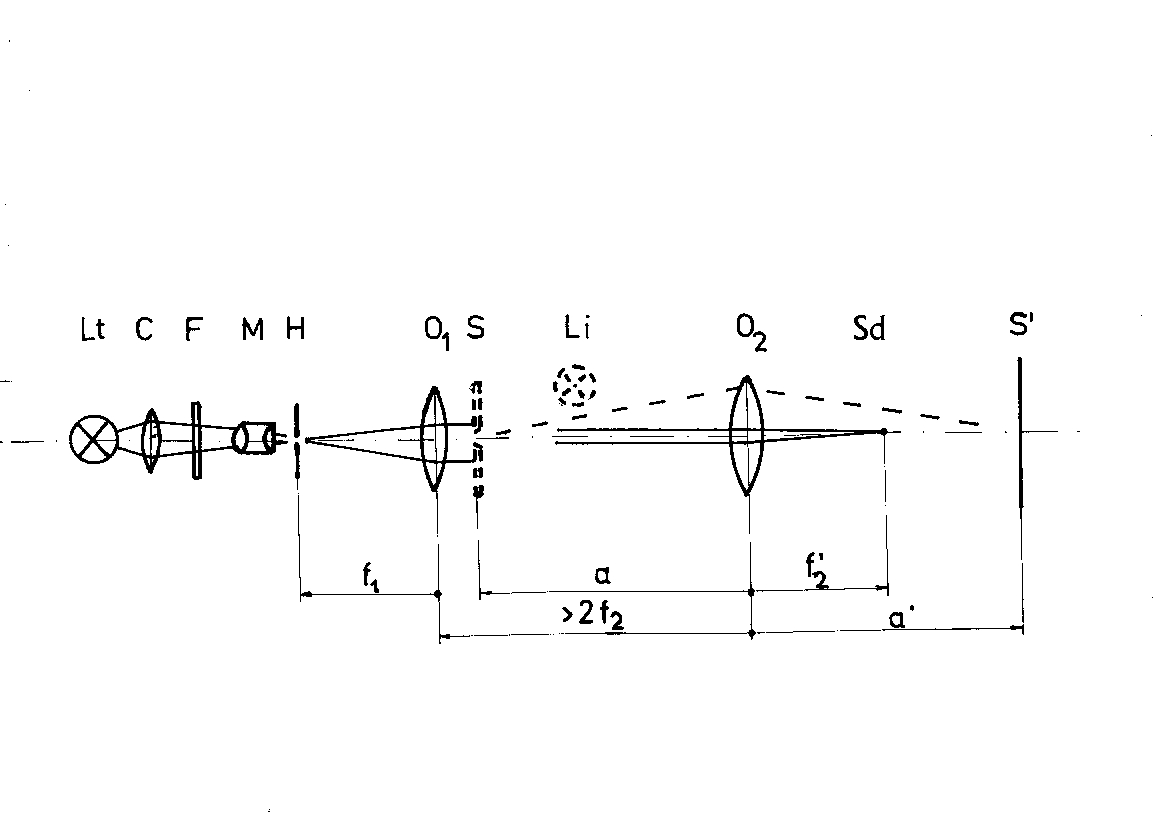
Figure 1. Experimental arrangement for diffraction experiments in a schlieren-apparatus according to Abbe. Lt - light-source, a super-pressure mercury lamp or a laser. C - condenser f' 0.90 mm; (F - filter for mercury lamp); H - hole-diaphragm in the image of Lt pinhole diaphragm Ø 1 ... 0,1 mm; O1 - lens 1; objective f' = 400 mm; S- diffraction slit or half-plane; Li - incident light source; O2 - lens 2, objective f' = 400 mm; SD - schlieren-diaphragm, less larger as H'; S' - image of S, this image is to view with a magnifier or the place of photo-plane or television-layer. Dot-lines shall indicate bent light
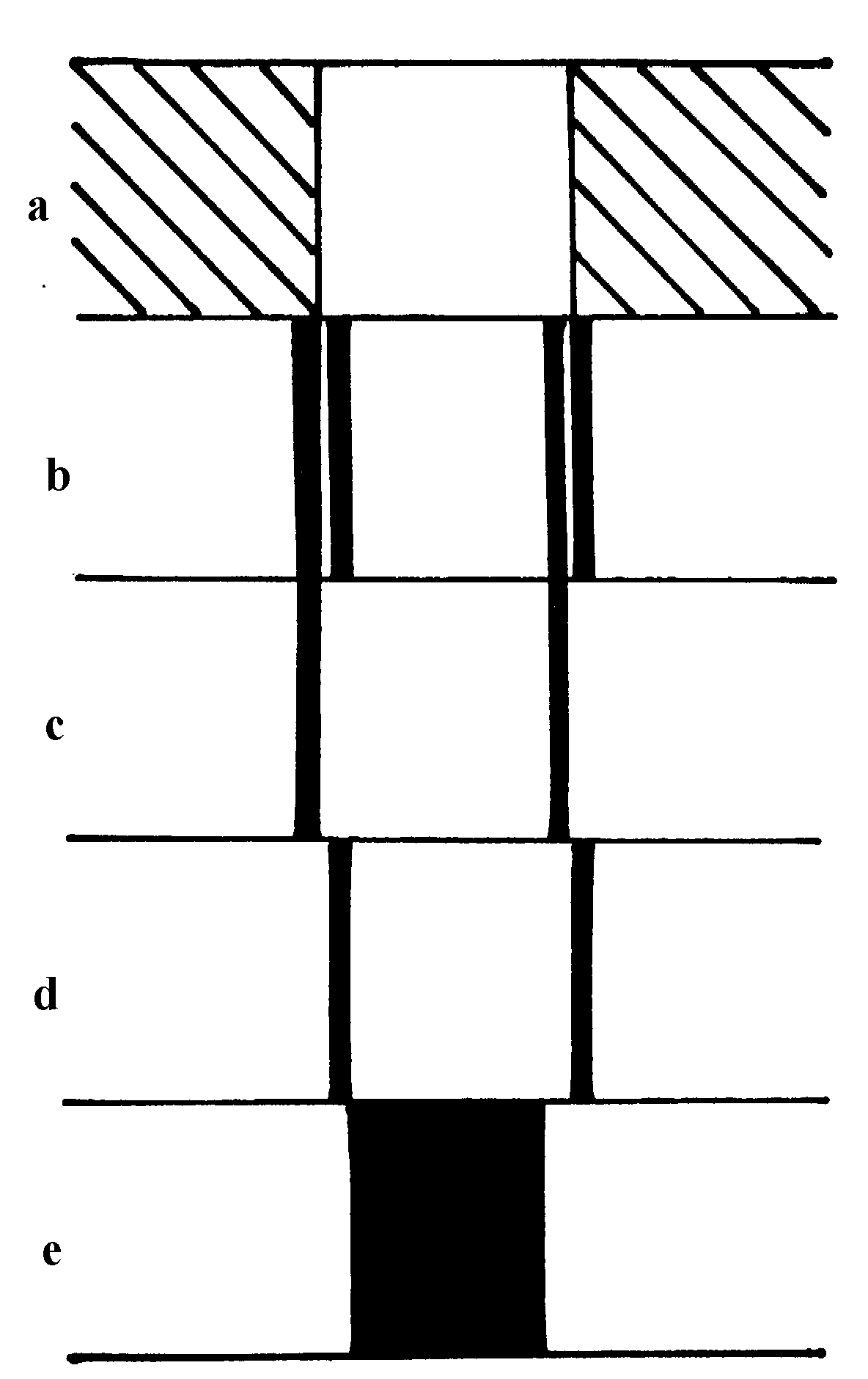
Figure 2. Show experiment as line-drawing (negative) with apparatus figure 1.
a: image of a slit in incident light,
b: image of a slit in a schlieren-apparatus,
c: one side of the figure of diffraction is masked before O2,
d: the other side is masked,
e: negative schlieren-apparatus, instead schlieren-diaphragm a hole-diaphragm.
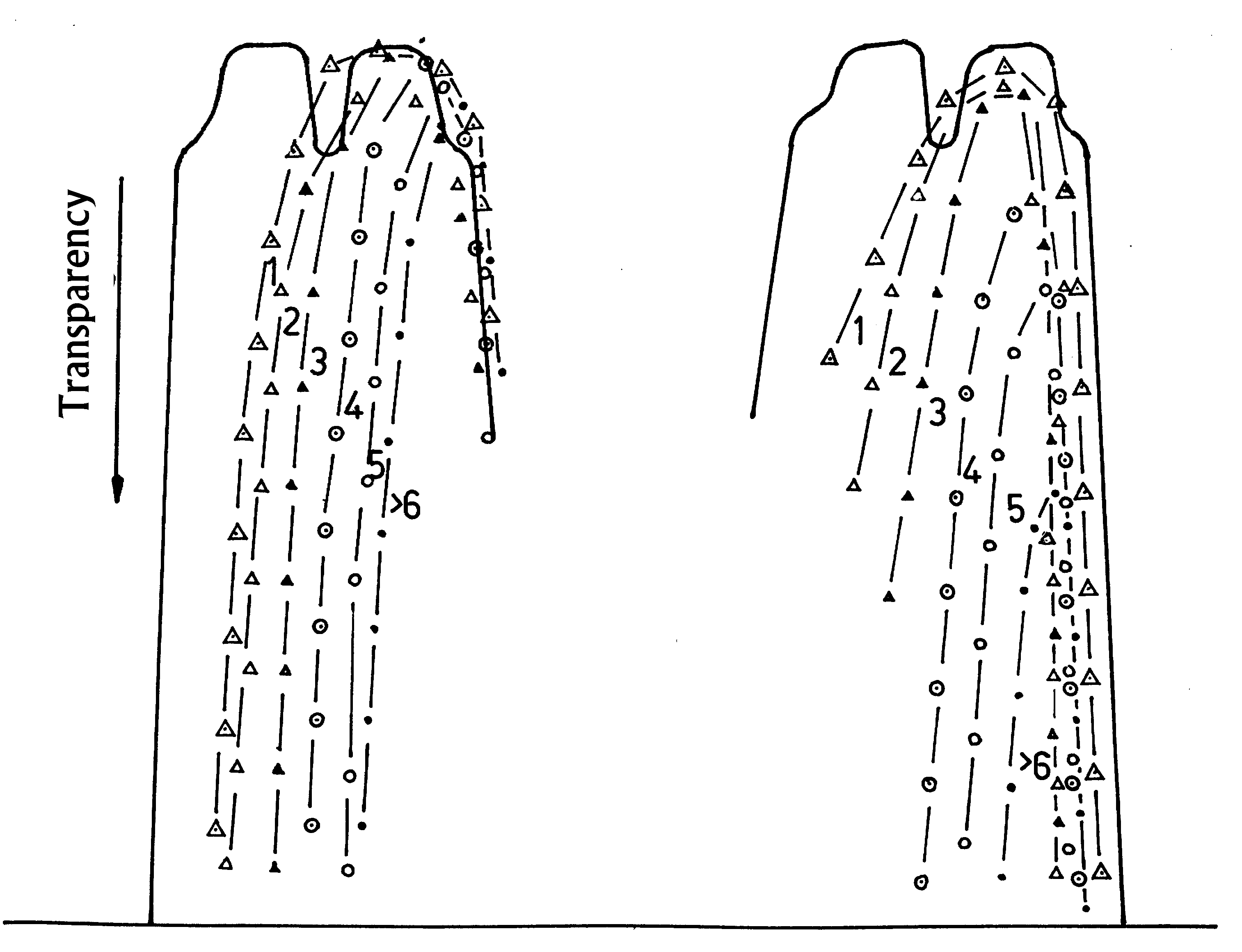
Figure 3. Photometer curves of the negatives of slit-images in the schlieren-apparatus figure 1 with partial masked diffraction figures in front of the lens O2. H: f 0.5 mm; S: slit 0.2 mm; a' : a = - 5. All negatives are equally exposed on the same plate one over another and taken with the same photometer setting. The diffraction fringes inside and outside the double stripes are left out because they are caused by diffraction at the schlieren-diaphragm or the mask plane. ● - more than half masked including the 5th order, ο - till the 4th order. ⊗ -till the 3rd order, ▲ - till the 2nd Δ - till the 1st order, ∇ - till the 0th order. Traced curves: the whole diffraction figure free.
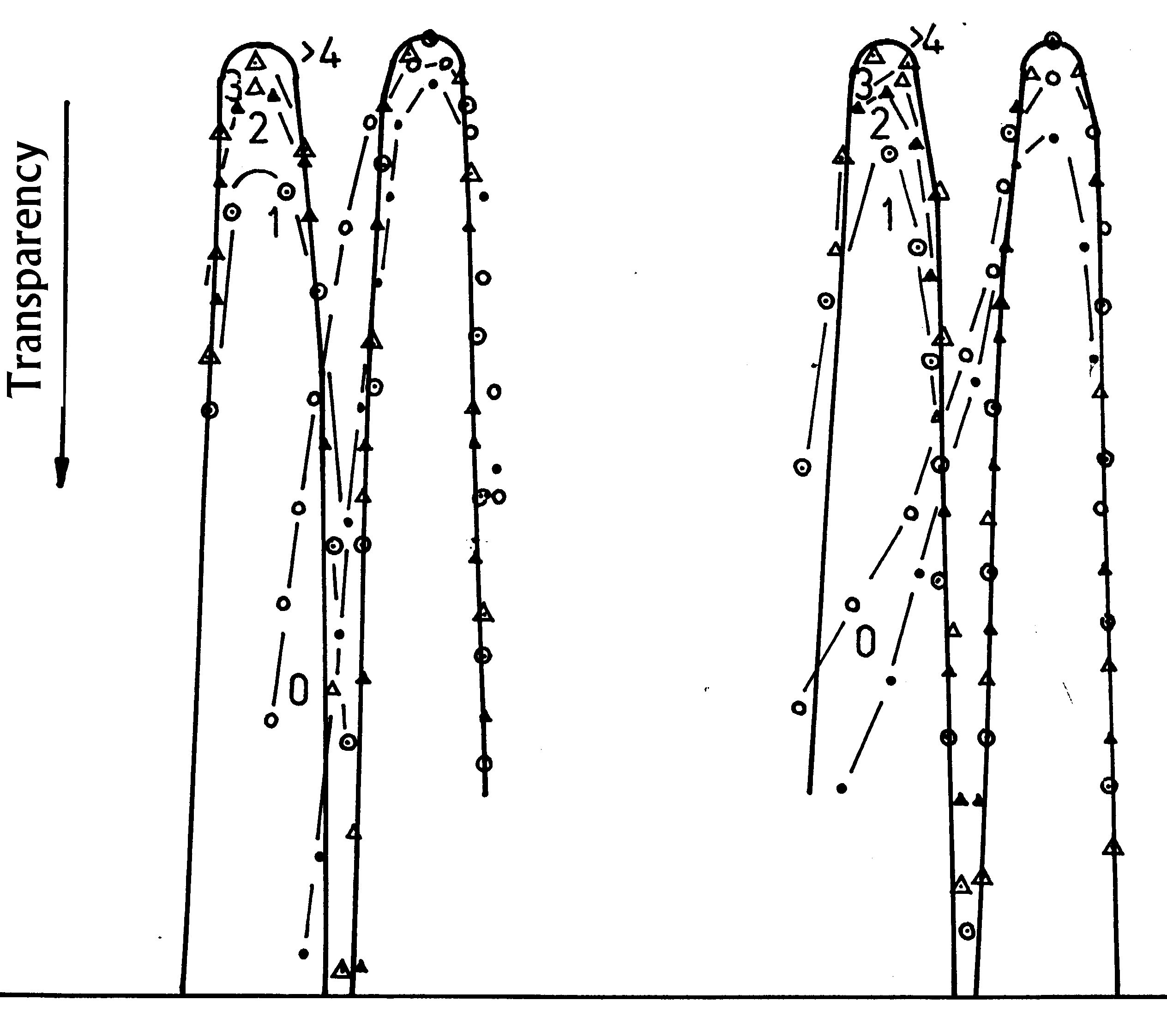
Figure 4. Photometer curves as figure 3 but with a new setting and a shorter exposure time. ● - one half and the 0th order masked, ο - one side and the 0th order free, ⊗ - additional the 1st order free, ▲ - additional the 2nd order free, Δ - additional the 3rd order free, ∇ - additional the 4th order free

Figure 5. Image of a slit 0.25 mm in a schlieren-apparatus figure 1 with a scale-ratio a' : a = 1 : -1. 30° oblique masked diffraction-figure before O2 , with 12 visible orders. O1 and O2 f' - 320 mm, the negatives are ten folds enlarged.
a: film in front of the overcrossing plane,
b: film close behind this plane.
General discussion
According to these facts one would ask the question why wave-theory of diffraction could keep so long. The answer is simple: Newton and his follower could not establish diffraction with light-particles, which are only thinkable as mass-points, for a force perpendicular to propagation-direction of light is not provided in Newton's mechanics. On the other side the wave-theory offered for large distance calculations and explanations were considered more importantly as the whole experimental security. To the begin of our century, as the quantum nature of light was discovered, one had to give Newton really right, but nothing was altered in the case of impossibility of explanation diffraction with punctiform particles of light or photons. So retained for diffraction Fresnel's wave-interpretation. Newton was right if he asserted that light never can be a wave, he had proved this with his proof of transformation of inner to outer diffraction fringes and the localization of bent light. Marshall [16] discussed the locality-debate. Newton's diffraction experiments brought the decisive experiments for local realism in diffraction. There are no doubts: The extrapolation of diffraction of outer fringes at the slit (formula (1) by Nieke [1]) to the distance nought or in the slit-plane was inadmissible and wrong.
The remark that for punctiform light-particles or photons as mass-points no explanation was possible, give the supposition that with space-filling, therefore with structure, seems possible an explanation. Indeed, off 1960 to all elementary particle are attached a structure, for it is to call the name of Hofstadter [17]. Also heavy elementary particles show the phenomenon of diffraction as for example reported by Carnal and Mlynak [18]. These particles have uncontested a structure that causes diffraction as deflexion, for nobody will suppose that atoms extinguish themselves.
First further experiments shall be put forward to obtain sufficient knowledge that permit an interpretation.
References
[1] Newtons Beugungsexperimente und ihre Weiterführung Halle 1997, Comp. Print 1, Arbeit 1 (vorhanden in vielen Deutschen Universitätsbibliotheken); H. Nieke, Newton's Diffraction Experiments and their Continuation. Halle 1997, comp. print 3, paper 1 (available in some university libraries).[2] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and (Colours of Light. London 1704); Opera quae exstant omnis, Tom IV, London 1782; Optics. Reprint Bruxells 1966; Optitk II + III, Übers. W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmann, Leipzig 1998; Neuauflage: Bd 96/97, Vieweg, Braunschweig 1983 Optique, Trac. J. P. Marat 1787; Bourgois, Paris 1989.
[3] A. J. Fresnel, Oeuvre Completes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926
[4] S. Banerji, Philos. Mag.(6) 37 (1919) 112.
[5] K. Noack, Phys. Z. 23 (1922) 228.
[6] M. v. Laue, in: Handbuch der Experimentalphysik Bd. 18 Akad. Verlagsges., Leipzig 1928, S. 349-350.
[7] H. K. V. Lotsch, Die Strahlenversetzung bei Totalreflexion: Der Goos-Hänchen-Effekt. Diss. T. H. Aachen 1970.
[8] K. H. Brauer u. F. Fröhlich, Experim. Techn. d. Physik 6 (1958) 216, Abb. 4.
[9] W. Heisenberg, Die physikalischen Prinzipien der Quanten- theorie. 2. Aufl., Hirzel, Leipzig. 1941. S. 9 - 14, 57 - 59; The physical principles of quantum theory, Univ., Press, Chicago 1930.
[10] H. Arndt u. H. Nieke, Z. Psychologie 193 (1985) 295.
[11] H. Nieke, Exper. Techn. Physik 31 (1983) 119.
[12] S. Ganci, Am. J. Phys. 57 (1989) 370.
[13] A. Rubinowicz, Ann. Physik (4) 53 (1917) 258; 73 (192.7) 339.
[14] Ch. Hofmann, Fortschr. Physik 27 (1979) 595; Exper. Techn. Physik 28 (1980) 403.
[15] K. Knop, Phys. Bl. 47 (1991) 901, Zitat S. 904.
[16] T. W. Marshall, Found. Phys. 22 (1992) 363.
[17] R. Hofstadter, Rev. Mod. Phys. 28 (1956) 214; Phys. Bl. 18 (1962) 193.
[18] O.Carnal u. J. Mlynek, Phys. Bl. 47 (1991) 379; Phys. Rev. Lett. 66 (1991) Nr. 21, 2639-96.
© 2006 by tediamedia • info@gebeugtes-licht.de