
Newton's and Fresnel's Diffraction Experiments
The Continuation of Newton's Diffraction
Experiments
Diffraction of Light at Slit and Hindrance
Interference-Angle Condition, Diffraction and
Imagery
Diffraction One After Another and with
Intermediate Imagery
Diminishing of Frequency of Light after
Diffraction
Inner and Outer Diffraction-Fringes at
Circular Openings
Superposition of Interference and Diffraction
Diffraction Experiments with Inhomogeneous
Illumination
Experiments with Polarized Light at Slit and
Double-Slit
The Background of Diffraction-Figures
Trial for Interpretation of Newton's Diffraction
Experiments
Consequences for Photons out of Newton's
Diffraction Experiments
Consequences for Structure of Electrons out of
that of Photons
The Thermally Conditioned Electromagnetic Field
Diffraction and Light-Emission of Electrons
Energy-Steps of Electrons in Magnetic Eigen-Field
Faraday's Electro-tonic States
Near-Field Optics with Regard to Newton's
Diffraction-Experiments
Consideration of Magnetic Moment of Electron
in Quantum Theories

Interference-Angle Condition, Diffraction and Imagery
The so called coherence-condition contains a geometrical relation, where the angle to (conventionally) light-source has to be smaller than to interval of diffraction-fringes. Here an action of order of radiation does not exist, therefore the name interference-angle condition is offered. In Fraunhofer's manner of observation also inner diffraction-fringes of slit appears outside the focal-plane. At parallel incident light in distance of double focal length with and without optics the same diffraction figures with inner and outer fringes arise, only the figure is inverted with optics. Interference-angle condition and Abbe's theory of imagery complete one another in microscopic imagery.
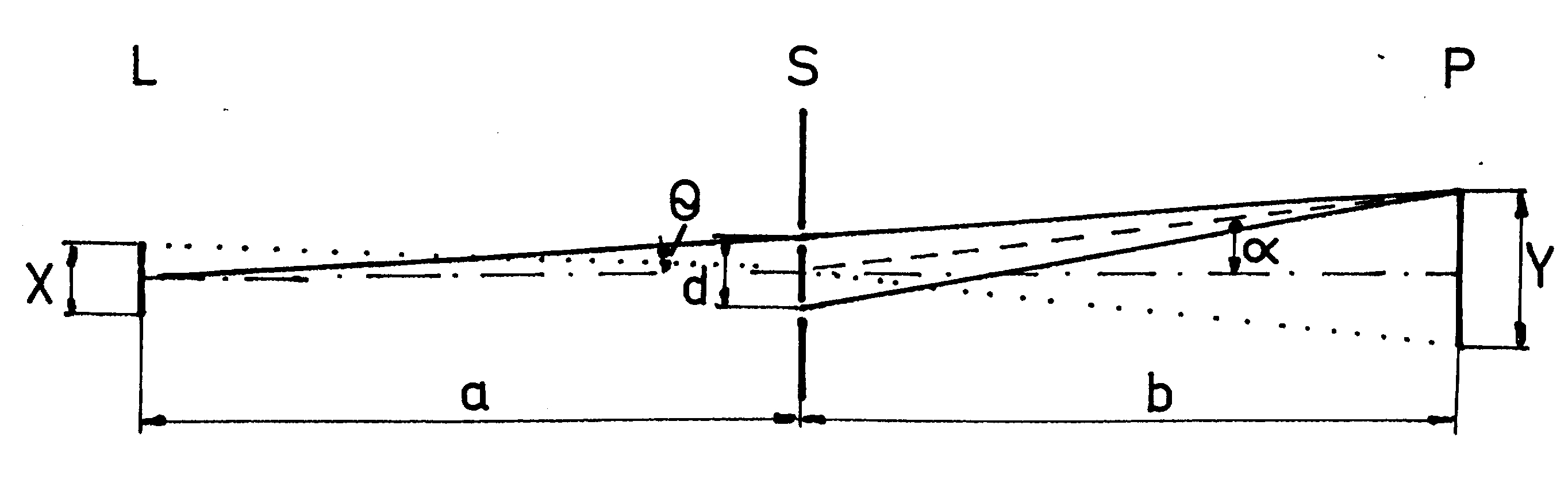
Figure 1. Schematic drawing of light-source and double-slit for derivation of the coherence-condition. L - light-source of the extend X; S - double-slit with the spacing d; P - photoplate with the first diffraction maximum in the spacing Y; Θ - half aperture-angle; α -diffraction-angle..
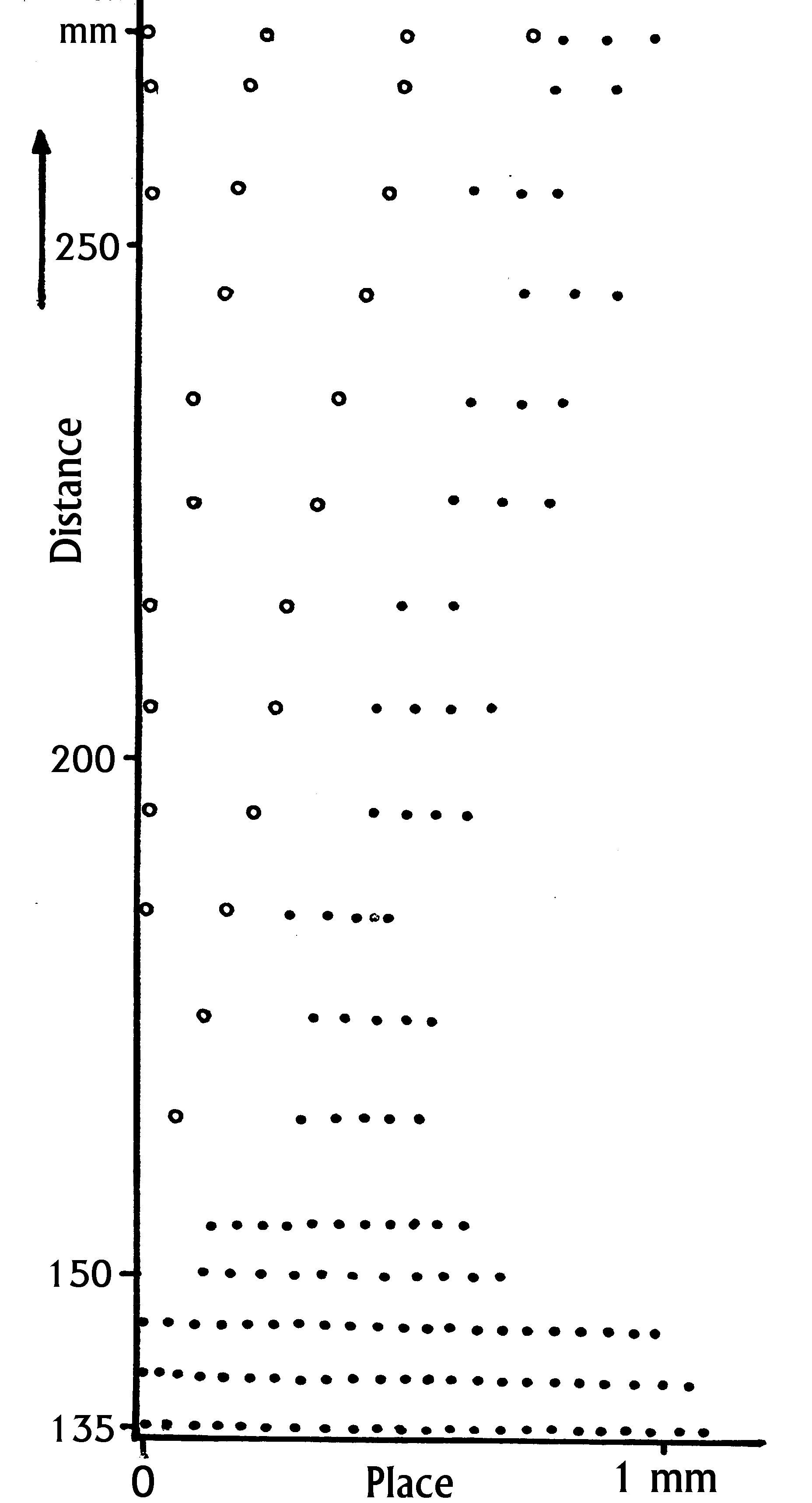
Figure 2. The positions of the maxima of inner and outer diffraction-fringes between single and double focal-length. 135 mm - single focal-length, 270 mm - double focal-length, ο maxima of inner fringes, • - outer- fringes. The outermost appearances of inner diffraction-fringes mark the shadow - limit.

Figure 3. Photometer-curves or diffraction-figures of a slit with a width of 0.6 mm. Illumination-slit 0.001 mm, tessar f' = 135 mm as collimator. a: without farther optics in 140 mm distance, b: with a lens f' = 140 mm in 140 mm distance.
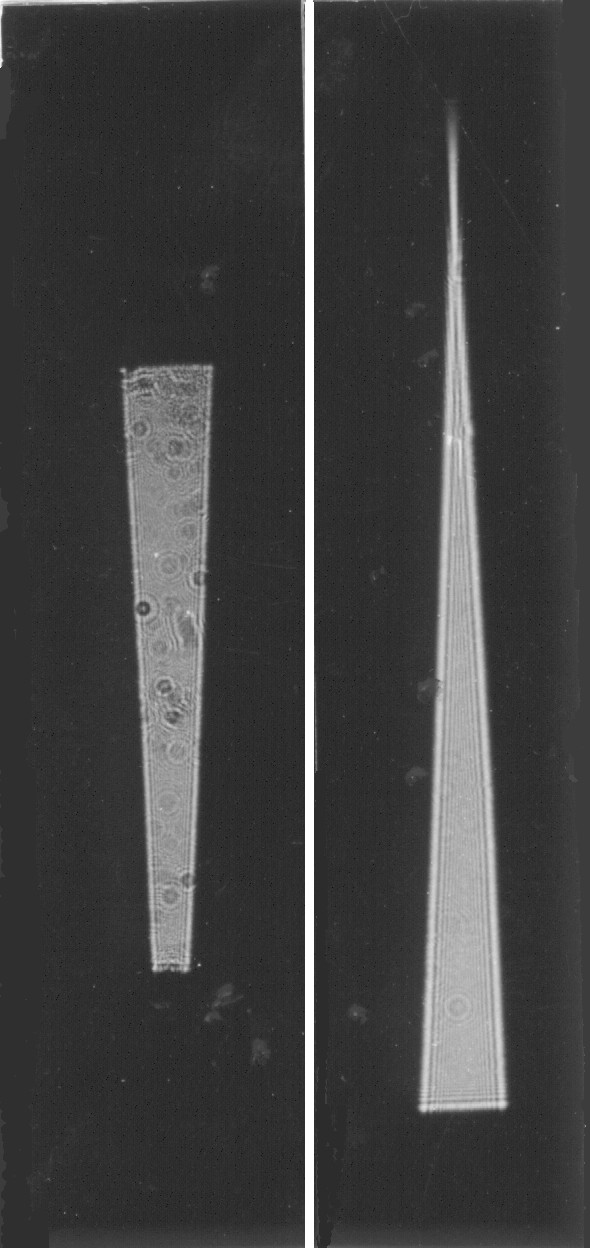
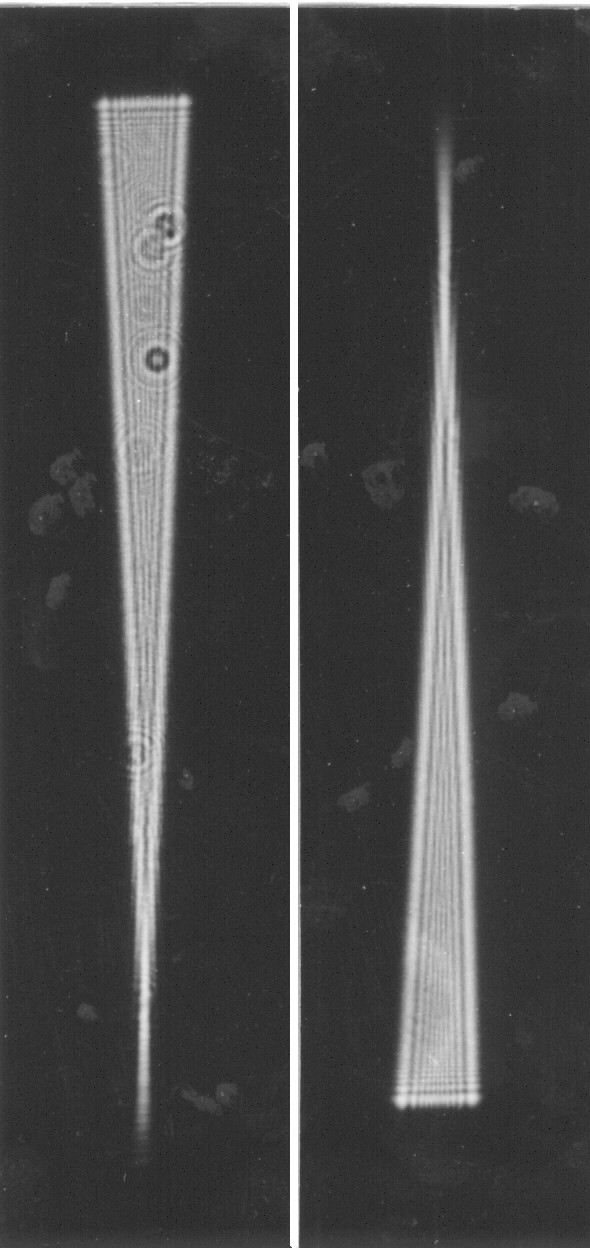
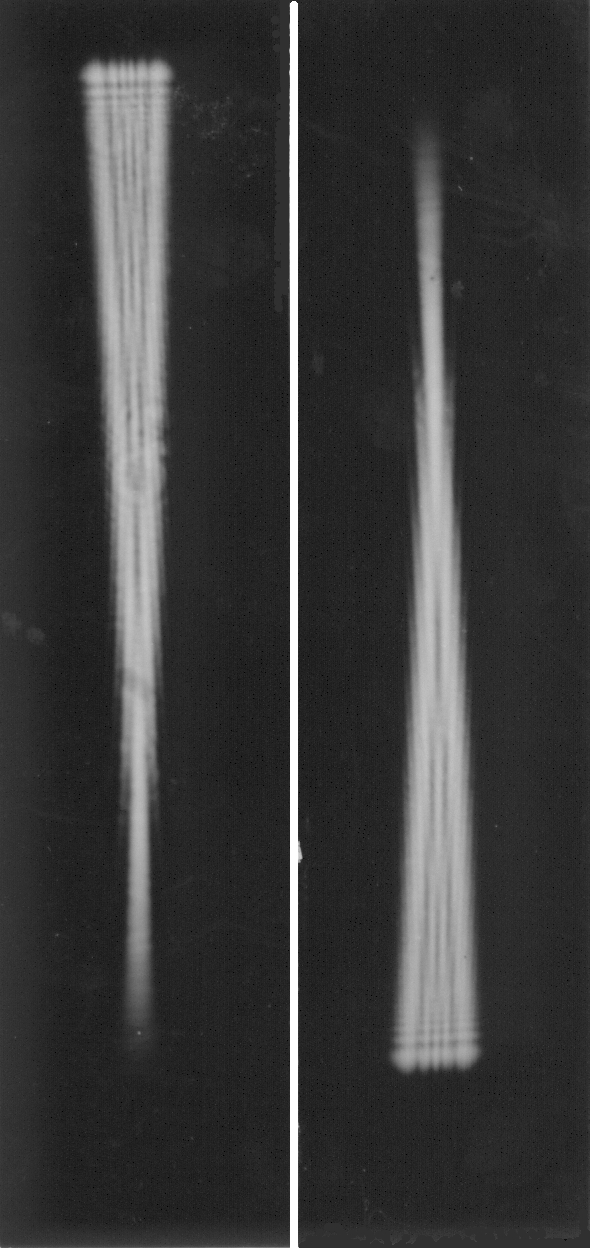
Figure 4. Diffraction-figure of the triangular-slit in double focal-length. A super-pressure mercury-lamp HBO 100 with green-filter and condenser that illuminated a hole-diaphragm 0.1 mm, in 1 m distance stood a lens f' = 1 m, behind that a triangular-slit 0 . . .3 mm that was so parallel illuminated. Behind: a: Tessar 1 : 2.8, f'= 50 mm, diffraction-figure in 100 mm distance, b: Objective removed, diffraction-figure in 100 mm distance.
Figure 5. As figure 4. a: Tessar 1:4.5, f'= 135 mm, diffraction-figure in 270 mm distance, b: Objective removed, diffraction-figure in 270 mm.
Figure 6. As figure 4. a: Achromat 1 : 8, ft = 320 mm, diffraction-figure in 640 mm distance. b: Objective removed, diffraction-figure in 640 mm distance.
Discussion
The analogy to water-waves suggested former to accept light with order-states or phase-relations. Already Maxwell [30] considered light electro-magnetic disturbance, but he calculated also with waves. With help of interference-angle condition could be shown that there the wave-interpretation of the so called coherence-condition never was necessary for it is explicable pure geometrically.
At diffraction with imagery is to respect that inner and outer diffraction-fringes of slit show another dependence of distance. As generally known grow intervals of outer fringes linear with distance, photons run here rectilinearly. Differently there are the dependence of the inner fringes of slit or diffraction-fringes of the half-plane. Here Fresnel [19] found experimentally an other behaviour.
It will do to consider parallel incident light, where intervals of diffraction-fringes grow only with the root of distance (more exactly by Nieke [24]). Newton [20] concluded out of transition from inner to outer fringes at triangular-slits that light-particle have to run eel-like. By Nieke [22], [23] and [24] the shadow-side bent light is displaced shadow-side for it seams to come from the slit-jaw, photons have to run in an S-curve. So it is sure that diffraction and imagery are to describe differently by inner and outer diffraction-fringes. In section 5 are described special-cases.
Panarella [31] examined the non-linearity of photo-multipliers at smallest intensity. He used the diffraction-figure of a small hole-diaphragm and he found their fringes blurred by smallest intensity. He diminished the intensity of light with neutral-density-filters that are so arranged in optical-path that they could reduce the interference-angle-condition as result of scattering in this filter. Here-upon could hint the blurred fringes. Jeffers, Wadlinger and Hunter [32] confirmed this result with a small slit instead hole-diaphragm, but they used the same apparatus with diminishing by density-filters. Therefore here is to prove that this was no effect of reducing of interference-angle condition.
References
[1] M. E. Verdet, Ann. Sci. L'École Norm. Super. (Paris) 2 (1865) 291.
[2] E. Berge, Math. naturwiss. Unterricht 27 (1974) 326.
[3] W. Arkadiew, Phys. Z 14 (1913) 832.
[4] P. H. Cittert, Physica 1 (1934) 201.
[5] F. Zernicke, Physica 5 (1938) 785.
[6] S. I. Wawilow, Die Mikrostruktur des Lichtes. Akademie-Verlag, Berlin 1954, S. 62, 76 u. 84.
[7] G. T. Reynolds, K. Spartalian u. D. E. Scarl, Nuovo chim. 61 B (1969) 355.
[8] P. A. M. Dirac, Die Prinzipien der Quantenmechanik. Hirzel, Leipzig 1930. The Principles of Quantum Mechanics. Clarendon Press Oxford 1935, 1947, 1958.
[9] P. L. Kapitza u. P. A. M. Dirac, Proc. Cambridge Phil. Soc. 28 (1933) 297.
[10] H. Schwarz, Z. Phys. 204 (1967) 276; Phys. Bl. 26 (1970) 436.
[11] G. Magyar u. L. Mandel, Nature 198 (1963) 255.
[12] G. Richter, W. Brunner u. H. Paul, Ann. Physik (7) 14 (1964) 239.
[13] R. J. Glauber, Phys. Rev. 130 (1963) 2529; 131 (1963) 2766.
[14] J. F. Vinson, Optische Kohärenz. WIB 85, Akademie-Verlag Berlin, Pergamon Press, Oxford, Vieweg Braunschweig 1971.
[15] H. Nieke, Exp. Techn. Physik 31 (1983) 53.
[16] E. Schrödinger, Ann. Physik (IV) 61 (1920) 69.v [17] A. Einstein, Phys. Z. 18 (1917) 121.
[18] E. Schrödinger, Nature and the Greeks. Univ. Press Cambridge 1954; Die Natur und die Griechen. Rowohlt Nr. 28, Hamburg 1956, S. 35.
[19] A. J. Fresnel, Oeuvre Complétes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.
[20] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions, Inflexions and Colours of Light. London 1704.Opera quae extant omnis, Tom IV, London 1782; Optik II +III. Übers. W. Abendroth, 0stwald's Klassiker Nr. 97. Engelmann, Leipzig 1898; Neuauflage Bd 96/97, Vieweg, Braunschweig 1983; Optique, Trac. J. P. Marat 1787; Bourgois, Paris 1989
[21] J. v. Fraunhofer, Gesammelte Schriften. Verl. bayr. Akad. München 1888. [22] H. Nieke, Newtons Beugungsexperimente und ihre Weiter führung. Halle 1997, Comp. Print 1, Arbeit 1 (vorhanden in vielen Deutschen Universitätsbibliotheken) Newton's Diffraction Experiments and their Continuation. Halle 1997, comp. print 3, paper 1 (available in some university libraries).
[23] As [22], paper 2.
[24] As [22], paper 3.
[25] F. Zernicke, Physica 9 (1942) 686. [26] F. T. S. Yu, in Ed. F. Wolf: Progress in Optics XXIII (1986) 222.
[27] K. Pietsch u. E. Menzel, Optik 12 (1955) 203.
[28] W. Messerschmidt, Optik 12 (1955) 297.
[29] E. Menzel, W. Miradé u. I. Weinberger, Fourieroptik und Holographie. Springer, Wien u. New York 1973, quotation in foreword.
[30] J. C. Maxwell, The scientific papers. Cambridge 1890; Hrsg. L. Boltzmann, Über physikalische Kraftlinien. Ostwalds Klassiker Nr. 102, Engelmann, Leipzig 1898.
[31] E. Panarella, Speculations Sci. Techn. 8 (1985) 35.
[32] S. Jeffers, R. Wadlinger a. G, Hunter, Can. J. Phys. 69 (1991) 1471.
© 2006 by tediamedia • info@gebeugtes-licht.de