
Newton's and Fresnel's Diffraction Experiments
The Continuation of Newton's Diffraction
Experiments
Diffraction of Light at Slit and Hindrance
Interference-Angle Condition, Diffraction and
Imagery
Diffraction One After Another and with
Intermediate Imagery
Diminishing of Frequency of Light after
Diffraction
Inner and Outer Diffraction-Fringes at
Circular Openings
Superposition of Interference and Diffraction
Diffraction Experiments with Inhomogeneous
Illumination
Experiments with Polarized Light at Slit and
Double-Slit
The Background of Diffraction-Figures
Trial for Interpretation of Newton's Diffraction
Experiments
Consequences for Photons out of Newton's
Diffraction Experiments
Consequences for Structure of Electrons out of
that of Photons
The Thermally Conditioned Electromagnetic Field
Diffraction and Light-Emission of Electrons
Energy-Steps of Electrons in Magnetic Eigen-Field
Faraday's Electro-tonic States
Near-Field Optics with Regard to Newton's
Diffraction-Experiments
Consideration of Magnetic Moment of Electron
in Quantum Theories

Superposition of Interference and Diffraction
In a Mach-Zehender interferometer is shown that the diffraction figure of a half-plane does not superpose with the interference figure of the half-plane undisturbedly. This is reduced because photons of the diffraction figure of half-plane do not go rectilinearly. The same fact is shown with Newton's rings where likewise diffraction and interference do not superpose undisturbedly. Whereas in scattering the superposition could not be examined, it was discussed why the common scattering figure can not originate in an usual interference apparatus.
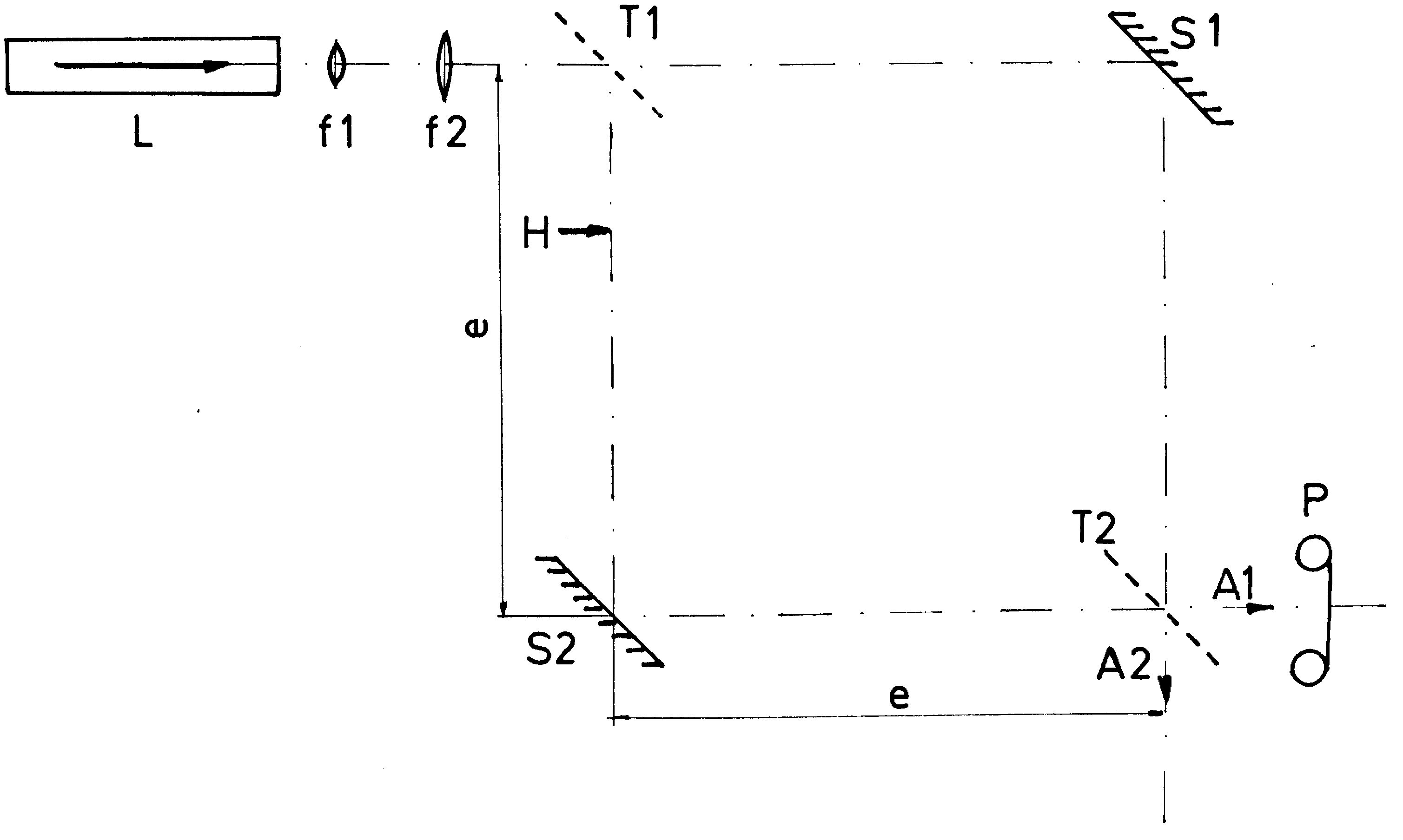
Figure 1: Mach-Zehender Interferometer (Leybold Didaktik). L - He-Ne-laser; f1, f2 - lens for beam-enlarging, parallel setting; T1, T2 -beam-splitters; H - in some photos place of half-plane or scattering-plate; e - distance 16.5 cm; S1, S2 - mirrors; Al, A2 - outlets, as positive and negative; P - corpus of a single-lens miniature-reflex camera.

Figure 2. Interference-figure of the interferometer according to figure 1
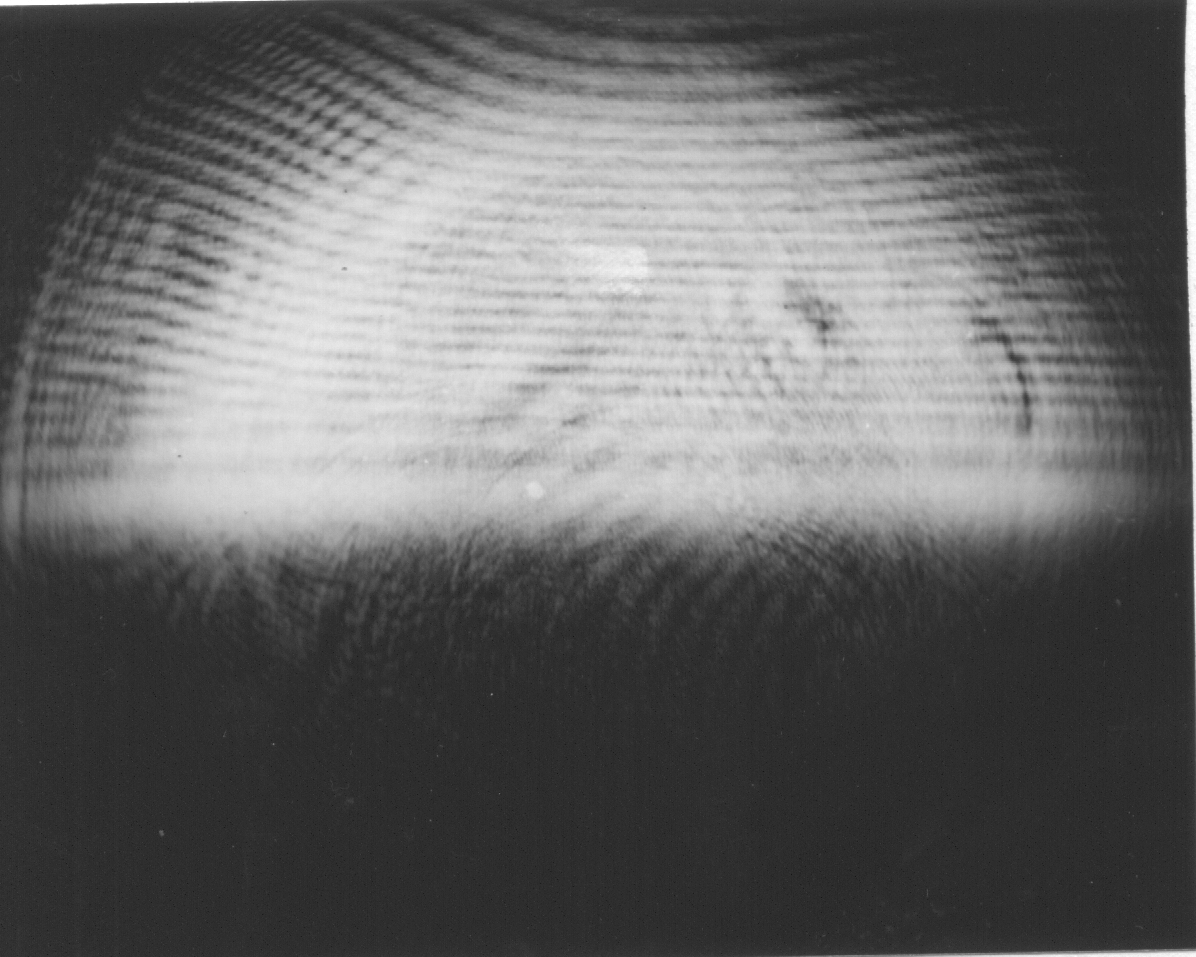
Figure 3. Diffraction-figure of a half-plane in H and masked other way of light.

Figure 4. Superposition of diffraction and interference.
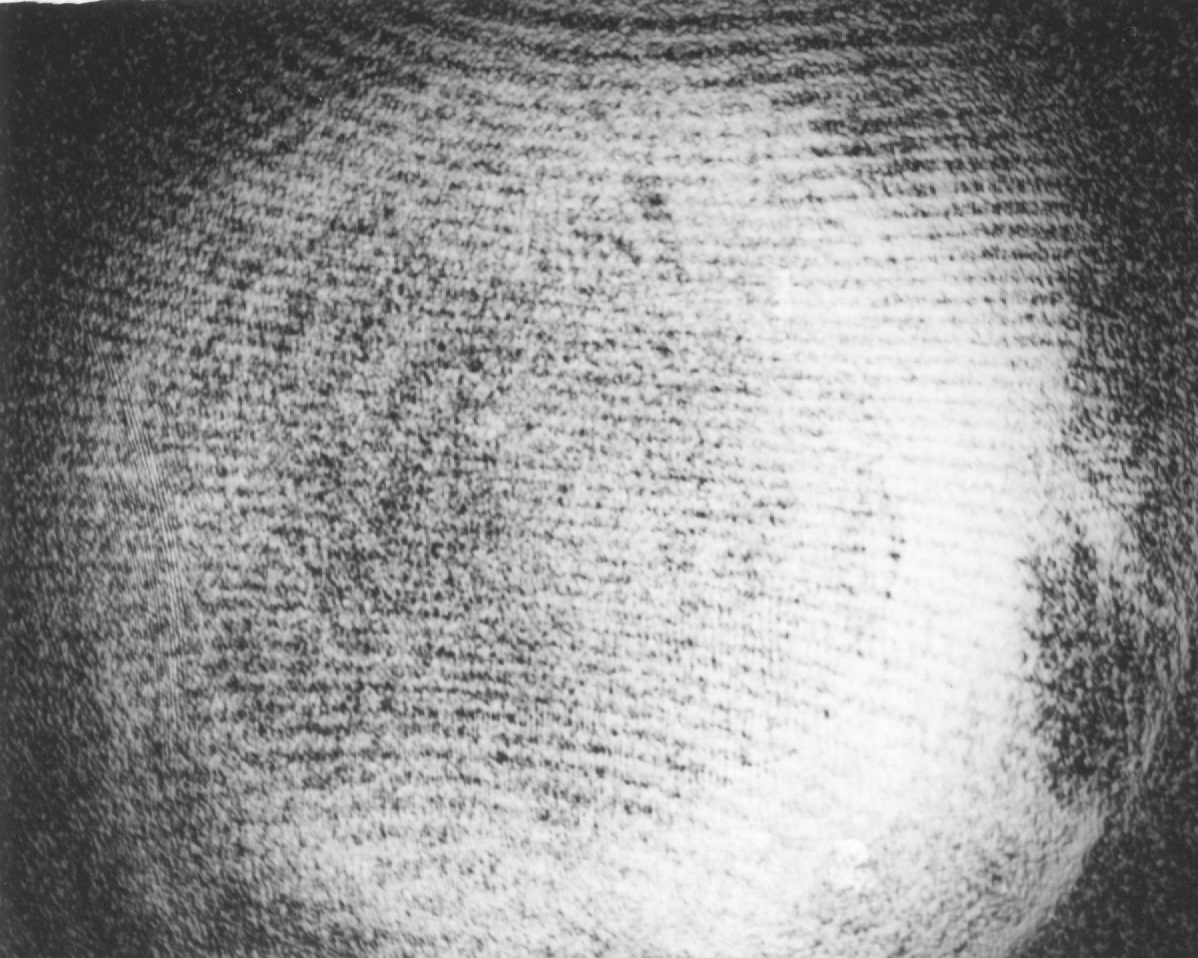
Figure 5. Undisturbed interference-figure with a limpid object-plane in H of figure 1, new adjusted
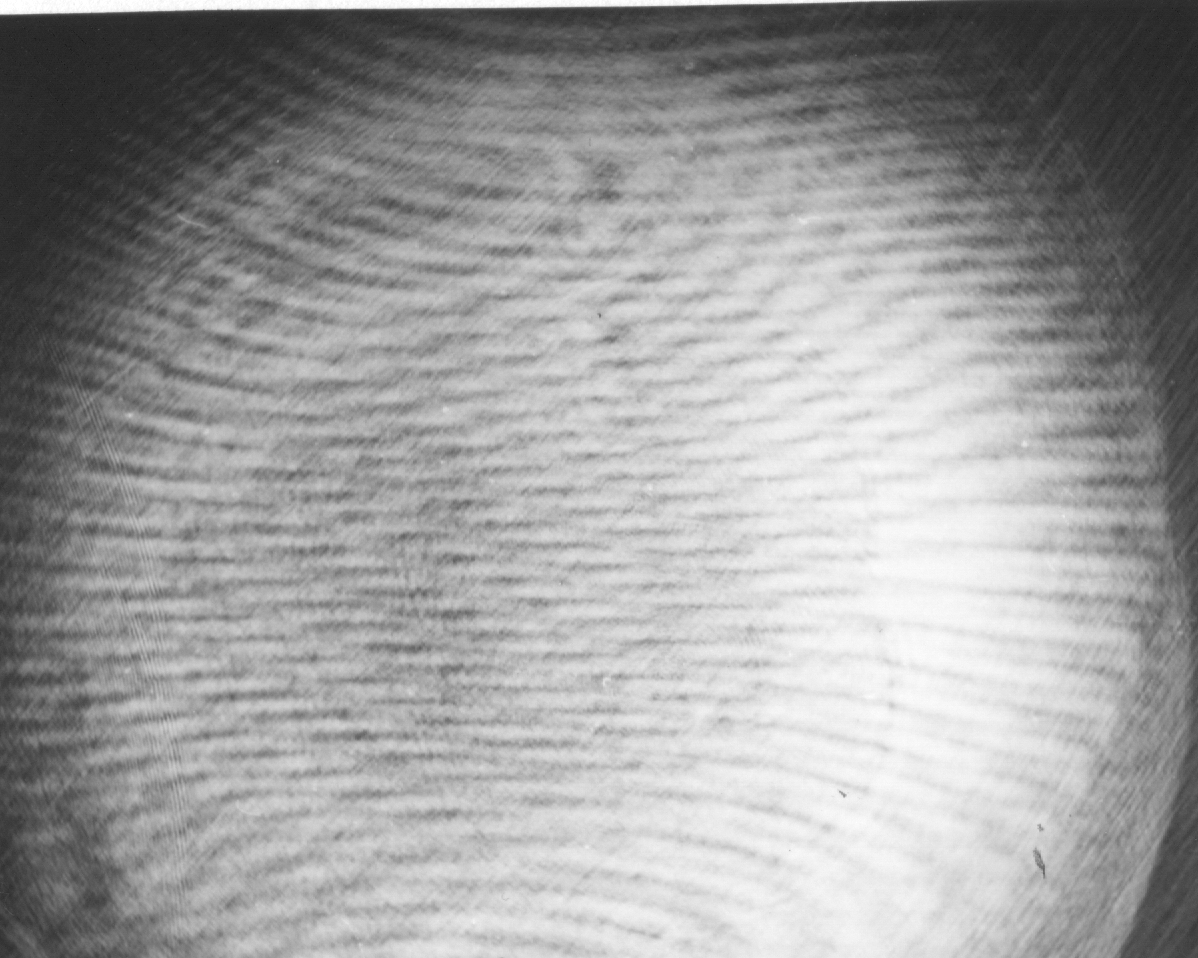
Figure 6. Scattering-figure with spores of ground-pine on an object plane in H, the other way of light was masked.

Figure 7. Whole-result with scattering-figure superposed of interference-figure.
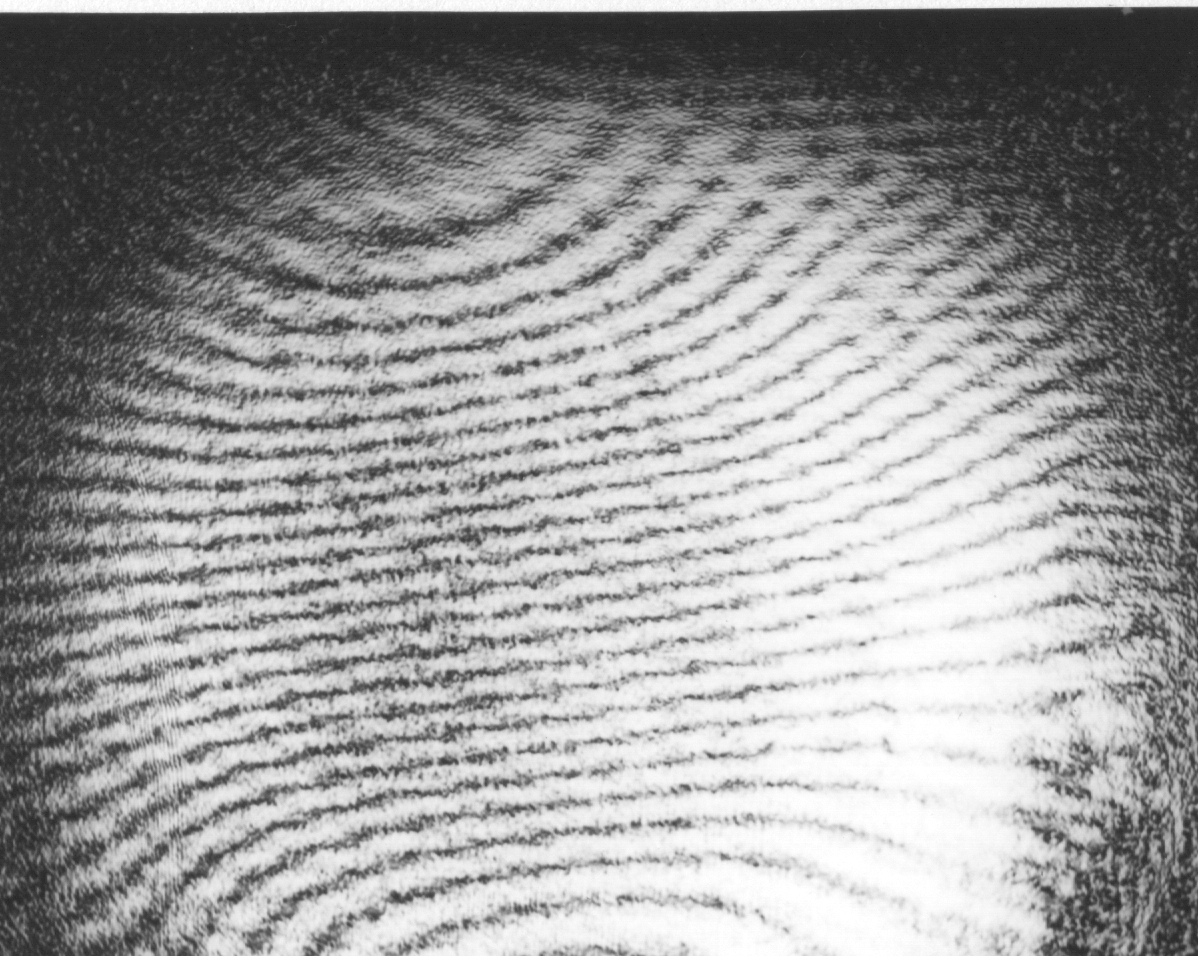
Figure 8. As figure 7, but the object-plane with spores of ground-pine moved additionally.
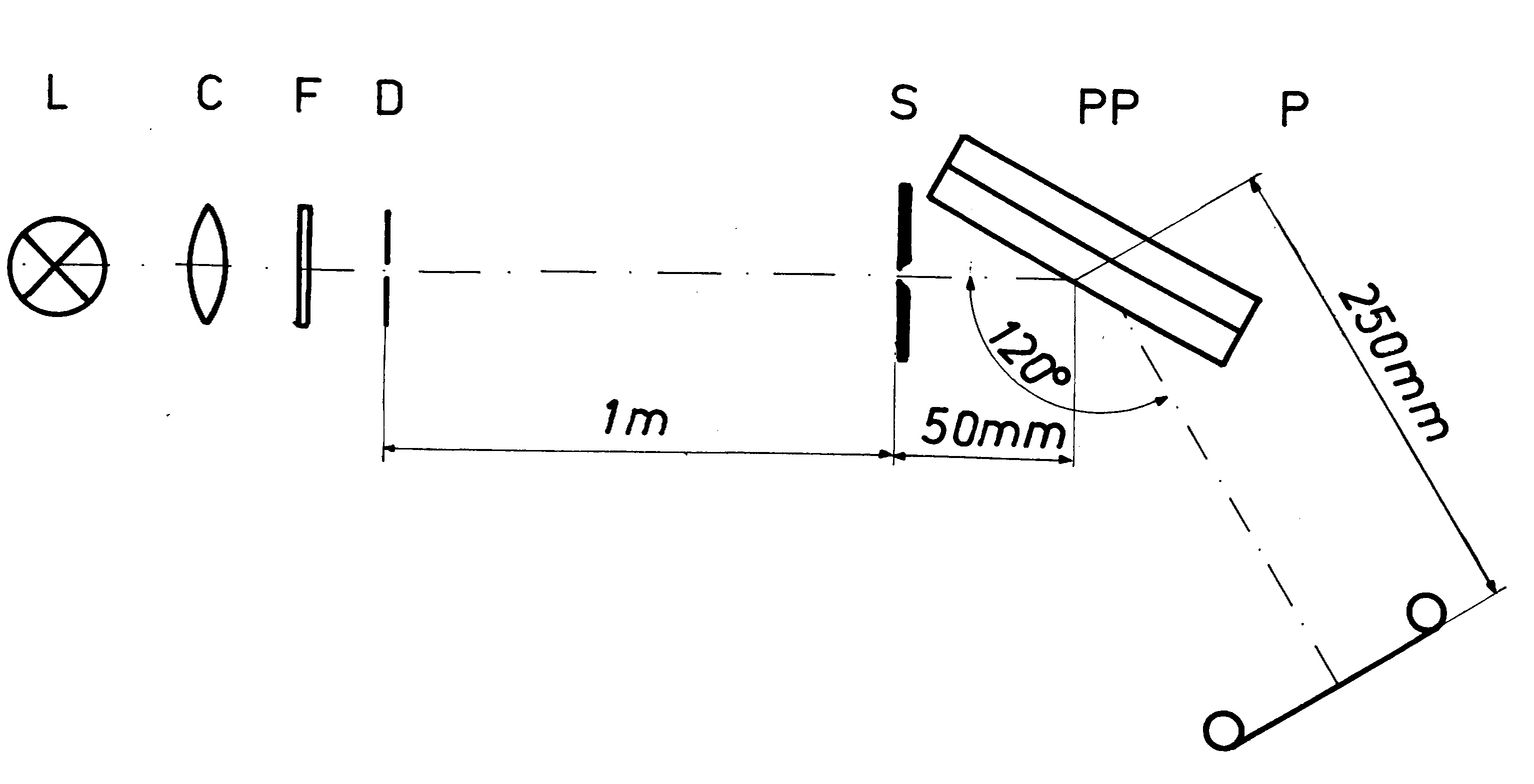
Figure 9. Experimental arrangement for examination of Newton's rings with illumination of diffraction-rings in reflection-position. L -light-source, a mercury-super-pressure lamp HBO 100; C - condenser; F - green-filter; D - circular-opening ~ 0.1 mm; S - variable slit; PP - plane-parallel plates that show Newton's rings; P - photo-film.

Figure 10. Parts of Newton's rings after Figure 9, illuminated with a slit-width of S with 2 mm. Arrows - cf. text.
Discussion of scattering experiments
For scattering at irregular particles usually used spores of ground-pine as for example Pohl [11] described with dusty mirror and irregular circular-openings. The there described scattering-figures are only visible if a small plane is illuminated and this is project on a large plane. In an usual interference-apparatus this scattering-figure is not to obtain, but only as in figure 6 scatter-particle are to see as points. Well, interferences are to show also in divergent light but this demand a special greater apparatus where light is lead convergent to H and then off H with scatter-plate divergent. This could be attempt.
Then is to quote Laue [12] who reported at irregularly arranged scattering-particle about a refuse of classical wave-theory.
He reported also about radial fringes that do not correspond to the theory, also Nieke [6] found star-like scattering-fringes. Laue[13] wrote (translated): "... for experiment and theory on this place are passed without took cognizance each other." In this paper he put against one another without to give a solution.
According Laue the so called wave-optics failed in scattering-figures but wave-optics failed also in Newton's diffraction experiments (Nieke [6] and [14]). With Fourier's theorem every piecemeal monotonous function is to perform approximately, so Fresnel could give solutions for specific cases. In case of need with help of an arbitrarily introduced phase-jump only because deviation of wave-theory with experimental results. Laue [12] wrote (translated): "We see in this a refute of classical wave-theory, which has proved true at all interference- and diffraction-appearances so excellently." Here Laue respected only the formal mathematical application of Fourier-theorem and not Newton's diffraction experiments ([8] book III observation 5 and 10 and Nieke [14]). Here Laue is nowhere quoted, exact so like Laue [15] did not quoted in his hand-hook article about diffraction Newton's diffraction experiments.
References
[1] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Halle 1997, Comp. Print 1, Arbeit 5. (Vorhanden in vielen deutschen Universitätsbibliotheken): Newton's Diffraction Experiments and their Continuation. Halle 1997, comp. print 3, paper 5. (Available in some university libraries).
[2] A. Fresnel, Oevre Complétes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926.
[3] W. M Honig, In: Hrsg. W. M Honig, D. W. Kraft, E. Panarella: Quantum Uncertainties. Nato AST Series B Vol. 162, Plenum Press N.Y., London 1987, S. 97: Summary of de Martini's Paper.
[4] H. Nieke, Exp. Techn. Phys. 31 (1983) 53
[5] As [1], paper 4.
[6] As [1], paper 2.
[7] As [1], paper 3.
[8] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions Inflexions and Colours of Light. London 1704; Opera quae exstant omnis, Tom IV, London 1782; Optics, Reprint, Bruxelles 1966; Optik II + III, Übers. W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmannn, Leipzig 1898; Neuauflage Bd. 96/97, Vieweg, Braunschweig 1983; Optique, Trad. J. P. Macat 1787; Bourgois, Paris 1989.
[9] L. de Broglie, La Physique quantique restera-t-elle indéterministe? Gauthier-Villars, Paris 1953; Phys. Bl. 19 (1953) 488, 541.
[10] E. Mach, Die Prinzipien der physikalischen Optik, Barth, Leipzig.1921. The Principles of Physical Optics. New York 1926
[11] R. W. Pohl, Optik. 8. Aufl. 1948 Springer, Berlin, Göttingen, Heidelberg S. 79 u. 107.
[12} M. v. Laue, Ber. Dtsch. Phys. Ges. 19 (1917) 19.
[13] M. v. Laue, Sitzungsber. Akad. Wiss. Berlin 1914 XLVII S. 1144.
[14] As [1], paper 1
[15] M. v. Laue, In: Handbuch der Experimentalphysik Bd 18. Akad. Verlagsges. Leipzig 1928.
© 2006 by tediamedia • info@gebeugtes-licht.de