
Newton's and Fresnel's Diffraction Experiments
The Continuation of Newton's Diffraction
Experiments
Diffraction of Light at Slit and Hindrance
Interference-Angle Condition, Diffraction and
Imagery
Diffraction One After Another and with
Intermediate Imagery
Diminishing of Frequency of Light after
Diffraction
Inner and Outer Diffraction-Fringes at
Circular Openings
Superposition of Interference and Diffraction
Diffraction Experiments with Inhomogeneous
Illumination
Experiments with Polarized Light at Slit and
Double-Slit
The Background of Diffraction-Figures
Trial for Interpretation of Newton's Diffraction
Experiments
Consequences for Photons out of Newton's
Diffraction Experiments
Consequences for Structure of Electrons out of
that of Photons
The Thermally Conditioned Electromagnetic Field
Diffraction and Light-Emission of Electrons
Energy-Steps of Electrons in Magnetic Eigen-Field
Faraday's Electro-tonic States
Near-Field Optics with Regard to Newton's
Diffraction-Experiments
Consideration of Magnetic Moment of Electron
in Quantum Theories

Inner and Outer Diffraction-Fringes at Circular Openings
In a schlieren-apparatus is shown that also at circular-openings bent light comes only from a small (<0.1 mm) surroundings of edges. It is important, also for circular-opening, to distinguish between inner and outer diffraction-rings, only in this way it is possible to comprehend the nature of diffraction. The differences of Fresnel's and Fraunhofer's manner of observation are demonstrated.
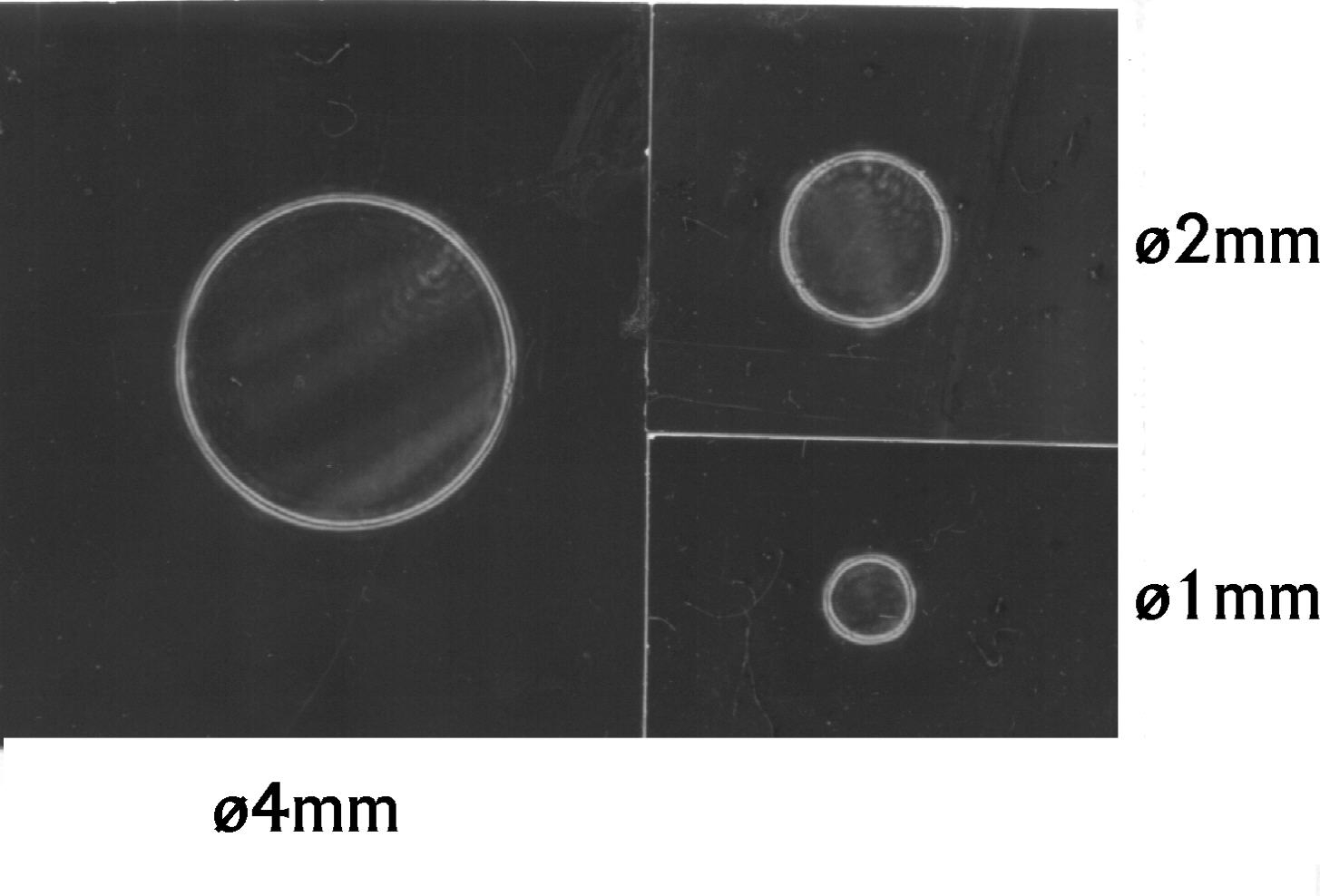
Figure, 1. Photos of circular-openings in a schlieren-apparatus. The circular-openings of the diameters of 1, 2 and 4 mm were drilled in an aluminium sheet and bevelled that only an edge about 0.1 mm was remaining which was blacken. Scale ratio 1 : 1 and optically enlarged.
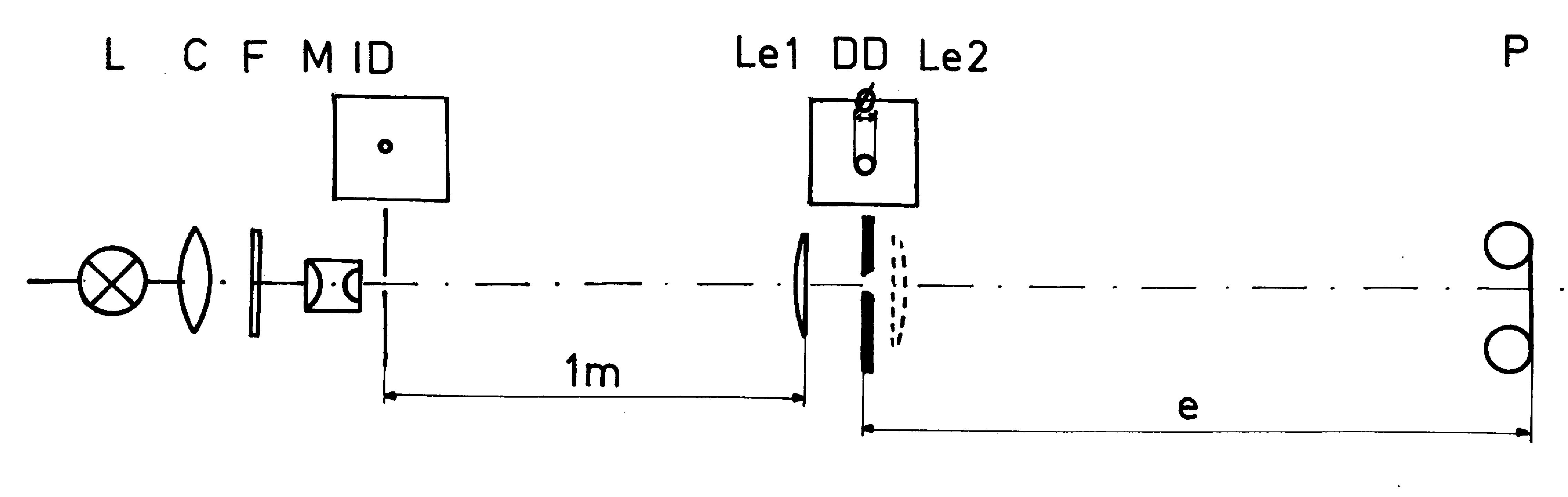
Figure 2. Experimental arrangement to examine the diffraction-figures of circular-openings in dependence of distance and of their diameter. L -light-source, a high-pressure mercury lamp HBO 100; C - condenser; F - green filter; M - microscope objective; ID - illumination diaphragm, a spinning-nozzle Ø 0.1 mm; Le 1 lens f' = 1 m; DD -circular diffraction diaphragm with diameters of 4, 2 and 1 mm; Le 2 - fallen off in Fresnel's observation manner, used with f'2 = e in Fraunhofer's observation manner; P - miniature reflex camera without optics

Figure 3. Diffraction-figures at circular-openings in the arrangement of figure 2. The upper halves of all photos show the rings in Fresnel's manner of observation with parallel incident light. Left above the drawing line for comparison are arranged the diffraction figures from the half-plane in the same distance. They are so below arranged that equivalent rings and fringes border together. Right and below this line as lower halves of half-photos are arranged the photos in Fraunhofer's manner of observation, thus is with the lens Le 2 with f'2 = e. The distance e in m is given left outside and the diameter of the used circular-opening DD in mm on the top./em>

Figure 4. Diffraction with and without imagery at circuit-openings in the arrangement of figure 2. Below rank: diameter of the used circular aperture in mm; left column: distance in m. The upper half of all photos are taken in Fresnel's manner of observation without the lens Le 2. The lower halves of the photos are taken with the lens Le 2 with a focal-length f' = 0.5 m. The first rank of photos shows the results in 0.5 m resp. in the focal-length. The second rank shows the results in 1 m distance resp. in the double focal-length, the third rank in 1.5 m resp. in the threefold focal-length.
General remarks to diffraction-rings at circular-openings
By Fresnel's manner of observation in short distances and large circular-openings originate inner diffraction-rings that correspond to inner diffraction-fringes of slit or diffraction-fringes of half-plane. The (unequal) intervals of diffraction-rings are non noticeable dependent in diameter of opening but only of distance, where by parallel illumination the intervals grow only with the root of distance as already Fresnel [6] found experimentally for half-planes. As Nieke [3] has proved, this dependence is valid first in distances greater than 105 λ (at visible light about 50 mm.), before the diffraction-figure of half-plane is erected.
However, in sufficient large distances or smaller openings outer rings instead of inner rings appear. Their intervals of rings harmonize with the intervals of rings, finding in Fraunhofer's manner of observation in the same distance, but with different intensities. They are proportional to the reciprocal diameter of opening. The transition from inner to outer in Fresnel's manner of observation (upper half in figure 3) takes place at f 4 mm between 1 and 2 m, at 2 mm f between 1/4 and 1/2 m and at 1 mm f between 1/16 and 1/8 m.
Whereas the intervals of outer diffraction-fringes at the slit are constant, so is that not the case at outer rings of circular openings, even if this is not so evident than in the intervals of fringes in half-plane or inner diffraction-fringes of slit. According Huygen's principle and integration over the circular plane with the radius R or outer diffraction-rings were calculated formally with the presupposition of large distances and not too great and not too small radii. With that (and only then) these outer rings were calculated by means of Bessel-functions
sin α = χ λ / R (1)
for minima χ = 0,61, 1,116, 1,619 ...
and for the maxima χ = 0,819, 1,346, 1,850 ... .
The derivation from constancy is small but notable.
Deviations from all calculations by wave-hypothesis appear at size of slit or diameter of circular-openings at smaller than 0.1 mm. Hönl, Maue and Westphal [8] quoted many formal or approximate estimations for this case. By Nieke [2] and [3] at slit width of 0.1 mm touch the two spheres from which bent light is coming. So a physical argument can be given because here at small slit-widths or circular-openings must rule other conditions. Here the presupposition of (inadmissible and wrong) extrapolation (cf. Nieke [9]) of formula for diffraction at slit with outer fringes in the slit-plane was fulfilled, that bent light has to come from the whole slit, but just here the calculation does not agree.
Fresnel's zone-construction describes a system of rings in the plane of diaphragm where the way of light from light-source to test-point grows respectively for λ / 2. Sommerfeld [10] wrote to that (translated): "A very descriptive, if only qualitative understanding, of these results yields the construction of Fresnel's-zones". This theory constructs a system of rings that yield only in special cases the right radius of diffraction-rings.
References
[1] I. Newton, Opticks, or a Treatise of the Reflexions, Refractions Inflexions and Colours of Light. London 1704; Opera quae exstant omnis, Tom IV, London 1782; Optics, Reprint, Bruxelles 1966; Optik II + III, Übers. W. Abendroth, Ostwald's Klassiker Nr. 97, Engelmannn, Leipzig 1898; Neuauflage Bd. 96/97, Vieweg, Braunschweig 1983; Optique, Trad. J. P. Macat 1787; Bourgois, Paris 1989.
[2] H. Nieke, Newtons Beugungsexperimente und ihre Weiterführung. Halle 1997, Comp. Print 1 Arbeit 2; (Vorhanden in vielen deutschen Universitätsbibliotheken); Newton's Diffraction Experiments and their Continuation. Halle 1997, Comp. Print 3, paper 2. (Available in some university libraries.
[3] As [2], paper 3.
[4] W. Arkadiew, Phys. Z. 14 (1913) 832.
[5] As [2], paper 4.
[6] A. J. Fresnel, Oeuvre Complétes I. Paris 1866; Abhandlungen über die Beugung des Lichtes. Ostwalds Klassiker Nr. 215, Engelmann, Leipzig 1926. [7] J. v. Fraunhofer, Gesammelte Schrift
en. Verlag bayr. Akad. München 1888
[8] H. Hönl, A. W. Maue u. K. Westphal, in: Handbuch der Physik Bd. XXV/1 Springer, Göttingen. Heidelberg, Berlin 1961.
[9] As [2], paper 1.
[10] A. Sommerfeld, Vorlesungen über theoretische Physik, Bd. IV Optik. Dietrich, Wiesbaden 1950 S. 222.
© 2006 by tediamedia • info@gebeugtes-licht.de